Курсовая работа: Определение основных характеристик системы передачи сообщений с дискретной фазовой модуляцией
При ДФМ Е0 = Е1 , поэтому алгоритм оптимального когерентного приема для двоичной системы можно записать: V1 >V0 ; при выполнении этого неравенства, принятым считается сигнал s0 (t), а при невыполнении этого неравенства принятым считается сигнал s1 (t).
Кроме того, т. к. при ДФМ информационный параметр сигнала определяется двумя соседними элементами [(n-1) – м на интервале [-Т; 0] и n-м на интервале [0; Т]], то оптимальный алгоритм следует записать в виде:
Приходящий сигнал s(t) на двух тактовых интервалах можно представить как:
(при передаче 0)
(при передаче 1)
После подстановки этих выражений в алгоритм получим алгоритм приема в виде:
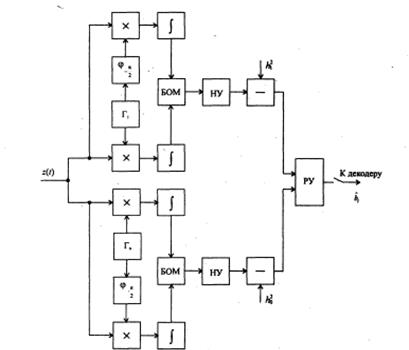
Рис. 8.1. Схема реализации оптимального приема дискретных сообщений при неопределенной фазе сигнала
X – перемножитель; Г – генератор опорных сигналов 
900 – преобразователь Гильберта; 
- интегратор; БОМ – блок определения модуля; РУ – решающее устройство.
3. Вероятность ошибки оптима