Курсовая работа: Определитель произведения прямоугольных матриц. Теорема Коши-Бине

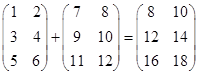
Опр. Пусть , , . Произведение скаляра на матрицу называется у которой в строке, столбце расположен элемент . Другими словами: Чтобы скаляр умножить на матрицу нужно все элементы матрицы умножить на скаляр .

Определение. Противоположной к матрице называется матрица

Свойства сложения и умножения матриц на скаляры:

-абелева группа

1) Сложение матриц ассоциативно и коммутативно.

2)

3)

а)

б)

4)

Глава II

§1 Умножение матриц

,

,

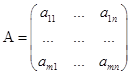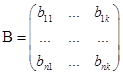
Опр. Произведением матрицы на матрицу называется матрица . , где

, где

Говорят, что есть скалярное произведение -строки матрицы на -столбец матрицы .

, где

Пример:

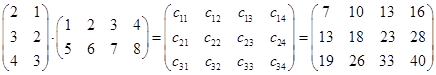
§2 Свойства умножения матриц

Умножение матриц ассоциативно:

1) , если определены произведения матриц и

Доказательство:

Пусть , так как определено , то и определено , то

Определим матрицы:

а)

б)

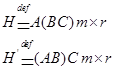(1) матрицы, тогда имеют одинаковую размерность