Курсовая работа: Определитель произведения прямоугольных матриц. Теорема Коши-Бине

Доказательство:

I) Перестановка столбцов:

Пусть - это матрица, полученная из перестановкой двух столбцов с номерами , где . Рассмотрим транспозицию:

, транспозиция является нечетной подстановкой , ,

В доказательстве будем использовать равенство:

Если пробегает все множество значений , то тоже пробегает все значения и

II) Перестановка строк

Пусть получена из перестановкой двух строк, тогда получена из перестановкой двух столбцов, тогда

III) Определитель матрицы, имеющий две одинаковые строки (столбца) равных нулю

Доказательство:

Проведем для такого поля , где

Замечание

Доказательство для случая найди в учебнике Куликовой Алгебра и теория чисел

Пусть в есть две одинаковые строки с номерами и , где , поменяем местами строки и , получим матрицу

(по св.2)

и , тогда

Если у два одинаковых столбца, то у транспонированной матрицы две одинаковые строки

IV) Если все элементы какой-либо строки (столбца) матрицы умножить на , то определитель умножиться на

Доказательство:

Пусть получена из умножением на строки

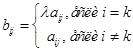
так как , то

Аналогичное доказательство для столбцов

V) Определитель матрицы у которой две строки (столбца) пропорциональны равны нулю

Доказательство:

Пусть в матрице , строки пропорциональны т.е -строка равна произведению на -строку. Пусть

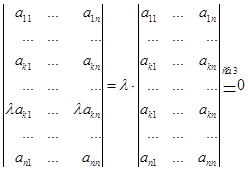
Для столбцов: