Курсовая работа: Определитель произведения прямоугольных матриц. Теорема Коши-Бине
Пример
Пусть 
-матрица 
, тогда 
-линейная комбинация строк матрицы 
коэффициенты которой служат элементы матрицы
Пример:
Столбцы матрицы 
-линейная комбинация столбцов матрицы 
. Строки -линейная комбинация строк матрицы 
.
§4 Транспонирование произведения матриц
поле скаляров, 
, 
, 
, 
Теорема
если 
, то 
. Обозначим: 
, 
Доказательство:
1) Пусть , 
- размерности 
,
- размерности , тогда 
и 
имеют одинаковую размерность
2) 
, 
-элемента расположенный в 
-строке, 
-столбце матрицы 
т.е 
, 
-произведение -строки транспонированной 
на столбец 
, 
Глава III
§1 Обратимые матрицы
поле скаляров, множество 
матриц порядка 
Определение. Квадратная матрица 
порядка называется единичной матрицей 
, 
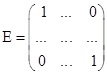
Пусть , 
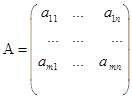
Теорема 1
, то для 
выполняется 
Доказательство:
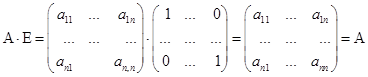
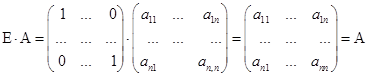
Из этого следует . Матрица является единичной матрицей. Она выполняет роль единицы при умножении матриц.
Определение. Квадратная матрица 
называется обратимой если существует 
так, что выполняются условия 
Матрица называется обратной к 
и обозначается 
, тогда если -это обратная к , то обратная к 
-это взаимообратные матрицы т.е.
Теорема 2