Курсовая работа: Основи метрології та вимірювальної техніки

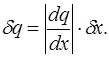(1.21)

4. В загальному випадку похибка функції декількох величин

,(1.22)

похибки яких незалежні і випадкові, знаходиться

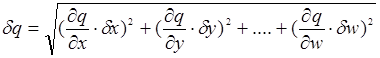,( 1.23)

але сумарна похибка ніколи не перевищить значення.

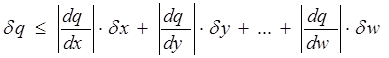.(1.24)

1.4 Оцінювання випадкових похибок сукупних та сумісних вимірювань

При сукупних та сумісних вимірюваннях невідомі величини хi , що підлягають безпосередньому вимірюванню, визначають за результатами вимірювання інших величин, які функціонально пов'язані з ними

φ(х1, х2, ... ,хn) =yj, (1.25)

де і=1, 2,....., n - порядковий номер невідомих величин х; j=1,2,...m - порядковий номер прямих вимірювань величин у.

Якщо результати прямих вимірювань Y містять випадкові похибки, то вони мають місце і в результатах сукупних (сумісних) вимірювань величин хi.

Розглянемо три випадки.

1. Очевидно, що для m < n систему розв'язати неможливо.

2. Для m=n розв'язання можливе, але похибки результатів вимірювання величин хi будуть, як і для прямих одноразових вимірювань, значними і числові значення цих похибок залишаються невідомими.

3. Для m>n систему знову неможливо розв'язати алгебраїчно тому, що ці рівняння несумісні, оскільки праві частини рівнянь замість точних значень Yj містять результати їхніх вимірювань уj= Yj + ΔYj; із випадковими похибками ΔYj,.

Проте у останньому випадку для нормального закону розподілу похибок вимірювання величини уj можна знайти таку сукупність значень xі, яка з найбільшою ймовірністю задовольняла б початкові умови φ(х1, х2, ... ,хn) =yj. Це можна здійснити за допомогою методу найменших квадратів (принципу Лежандра).

Такий спосіб обробки експериментальних даних для сукупних (сумісних) вимірювань доцільно застосовувати для лінійних функцій. В інших випадках обробка результатів значно ускладнюється.

Тому розглянемо випадок, коли функції φj лінійні

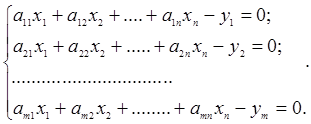(1.26)

Цю ж систему представимо більш компактно

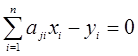, j=1,2,…m.(1.27)

Тут індекси при коефіцієнтах а показані у послідовності «рядок-стовпець».Ці рівняння називаються умовними. Через наявність похибок праві частини рівнянь дорівнюють не нулю, а деяким залишковим похибкам

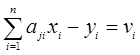, j=1,2,…m. (1.28)

Згідно з принципом Лежандра найбільш імовірними значеннями невідомих величин хі для цього випадку будуть такі, для яких сума квадратів залишкових похибок мінімальна

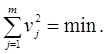(1.29)

Необхідною умовою такого мінімуму повинна бути рівність нулю похідних

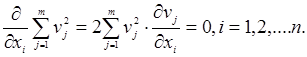(1.30)

Підставивши в формулу значення , отримують систему нормальних рівнянь

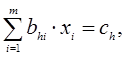
,(1.31)