Курсовая работа: Основи метрології та вимірювальної техніки
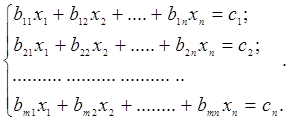(1.32)
Тут індекси при коефіцієнтах b показані у послідовності «рядок-стовпець» (h-і).
Оскільки кількість нормальних рівнянь завжди дорівнює кількості невідомих, то така система має розв'язок.
Загальний спосіб знаходження системи нормальних рівнянь полягає y знаходженні часткових похибок від кожної 
по кожній з невідомих хi , перемноженням цих похідних на відповідні значення та додаванні їх для кожної невідомої хі
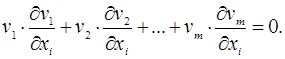(1.33)
Сукупність даних виразів представляє собою систему з n нормальних рівнянь.
Припустимо, що в результаті сукупних (сумісних) вимірювань отримай таку систему
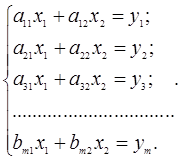(1.34)
Система нормальних рівнянь матиме вигляд
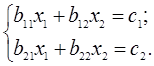(1.35)
Коефіцієнти 
визначають із таких виразів
; 
; 
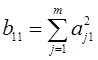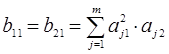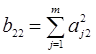.(1.36)
Тоді значення 
визначають
; 
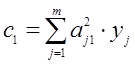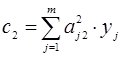.(1.37)
Якщо кількість невідомих n< 4, то систему нормальних рівнянь доцільно розв'язувати за допомогою визначників. Розглянемо розв'язування систем нормальних рівнянь для n = 2 .
У цьому випадку складають та обчислюють головний визначник цієї системи рівнянь
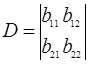.(1.38)
Далі складають та обчислюють часткові визначники 
та D2, замінивши коефіцієнти 
при відповідних невідомих на вільні члени 
в системі рівнянь
; 
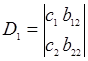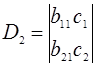.(1.39)
потім знаходять найбільш імовірні значення невідомих
; 
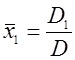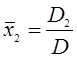.(1.40)
Середні квадратичні значення результатів сукупних (сумісних) вимірювань. Після підстановки найбільш імовірних значень 
до рівняння знаходять значення залишкових похибок визначають 
та суму квадратів залишкових похибок 
.
Середнє квадратичне відхилення результатів сукупних (сумісних) вимірювань знаходять за формулою
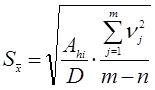,(1.41)
де m - кількість умовних рівнянь;
n - кількість невідомих;
- ад'юнкти (алгебричні доповнення) елементів 
головної діагоналі визначника D (для h=
). які отримують викресленням h-го рядка та і-го стовпця, відповідне даному елементу 
, з наступним до множенням на
(-1)h+1. Для n=2 ад'юнкти: А11=b22; А22=b11.
Задавшись значенням довірчої ймовірності, знаходять відповідне значення коефіцієнта довіри tр. У цьому випадку число ступенів свободи дорівнюють: