Курсовая работа: Основи метрології та вимірювальної техніки

;

.

.

;

=;

Розрахунки реалізовані за допомогою математичного пакету MathCAD і наведені у додатку Б.

2.3 Розв’язок завдання 3

Найкращою оцінкою багатократних прямих рівно точних вимірювань, що дає змогу зменшити вплив випадкових складових похибки вимірювання кожного окремого спостереження, є середнє значення

.(2.9)

Незміщена оцінка дисперсії сукупності спостережених значень

(2.10)

Проаналізуємо чи немає серед спостережень грубих (аномальних) помилок. Сформуємо із спостережень варіаційний ряд (від найменшого значення до найбільшого):

16,62; 16,62; 16,63;16,66;16,68;16,69;16,72;16,73;16,73;16,77;16,79;16,79;

Перевіримо крайні члени ряду на аномальність. Знайдемо співвідношення

(2.11)

(2.12)

За табл.1 (додаток), що задає допустимі значення про нормованих відхилень від середнього і заданою довірчою ймовірністю, знайдемо , а саме: для , а отже, надійності , та n=12 маємо . Оскільки та менші від , то кратні значення (варіанти) варіаційного ряду не треба розглядати, як аномальні. Незміщена оцінка середньоквадратичного відхилення середнього значення

(2.13)

Оскільки кількість спостережень < 30, то при оцінюванні гарантійного (довірчого) інтервалу для похибки середнього доцільно скористатися не розподілом Гауса, а Стьюдента. За табл.. 2 (додаток), що задає допустимі значення гарантійного коефіцієнта для заданої гарантійної (довірчої) ймовірності, знайдемо відповідний коефіцієнт. А саме для n=12, =0,99, =3,055. Отже, результат вимірювання

(2.14)

2.4 Розв’язок завдання 4.

Похибку опосередкованого вимірювання шукаємо за похибками прямих вимірювань. Зокрема, відносна похибка , А абсолютна похибка непрямого вимірювання (див. задачу3)

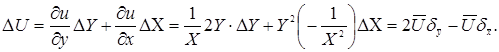(2.15)