Курсовая работа: Параметрическая идентификация динамических характеристик процесса формования изделий из композитов в автоклаве

где и

- коэффициент при пропорциональной и интегральной части.

Разомкнутая система регулирования имеет передаточные функции:

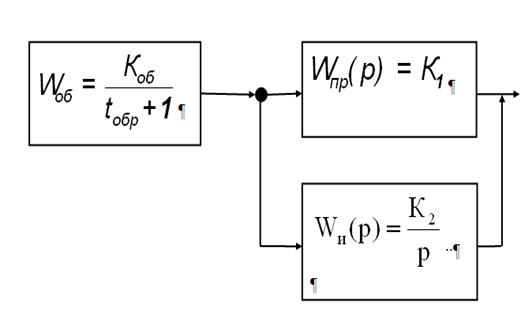
Рисунок 1 - Разомкнутая система регулирования.

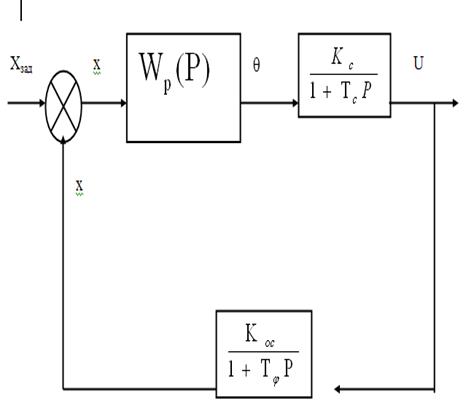
Рисунок 2 - Замкнутая система регулирования.

p– оператор Лапласа.

Только при условиях передаточная функция системы экспоненциальная, т.е. наиболее устойчива.

Если то передаточная функция примет вид:

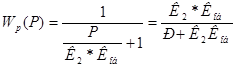
Передаточная функция замкнутой системы регулирования

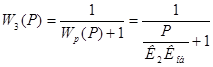
По аналогии передаточной функции RС фильтра коэффициент при операторе ф - постоянная времени.

Считаем что

Таким образом, имеются следующие выражения для определения отношения К1 и К2

;

Отсюда

;

г) Интегральная составляющая в ЭВМ вычисляется как выходная величина интегратора, на вход которого подана решетчатая функция DТ(t) значения которой фиксируются в моменты времени tn= Ту.

Ту - время между двумя измерениями температуры объекта.

Выходная величина интегратора запишется в виде выражения:

Для выражения Ки через К1 и К2 (3) приравняем выражение (4) и интегральную составляющую из (2) в значениях температуры:

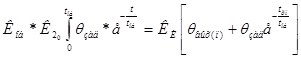
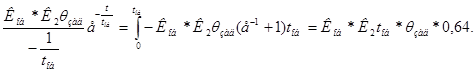
Этот безразмерный коэффициент используется в программе для деления интегральной составляющей по (4).д) При выбранных К1 и К2 и полученному из (5) Кд оценивается качество регулирования системы по трем показателей: