Курсовая работа: Параметрическая идентификация динамических характеристик процесса формования изделий из композитов в автоклаве

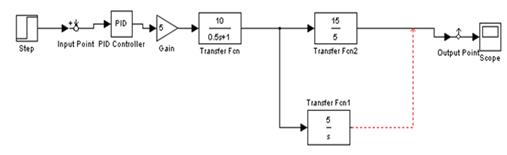
Рисунок 7 - Структурная схема САУ (разомкнутая) системы с помощью matlab

6. Проверка качества САУ

Устойчивость — это свойство САУ возвращаться в заданный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Устойчивость по Ляпунову

Впервые свойства устойчивости были исследованы русским ученым А.М.Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Он ввел понятия возмущенного и невозмущенного движений, асимптотически устойчивого движения. Теоремы А. М. Ляпунова позволяют судить об устойчивости нелинейных реальных САУ по их линеаризованным уравнениям.

По Ляпунову, если корни дифференциального уравнения линеаризованной системы содержат только отрицательные вещественные части, то линеаризованная система является устойчивой (невозмущенное движение асимптотически устойчиво) и никакие добавки в виде членов с различными нелинейностями не могут сделать систему неустойчивой. Определяя устойчивость линеаризованной системы, можно говорить и о свойствах устойчивости реальной системы. По расположению корней (Рисунок 8) понятно что исследуемые система является устойчивыми.

На рисунке 9 изображена АФЧХ системы, с помощью которой можно определить критерии устойчивости по теории Найквиста.Этот критерий называется точечным критерием (предложен в 1932 г. американским ученым Г. Найквистом). Он позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутой системы. В ТАУ этот критерий был по-новому обоснован, обобщен и применен Михайловым в 1938 г., поэтому еготакже называют КУ Найквиста—Михайлова. АФЧХ разомкнутой САУ можно получить как аналитически, так и экспериментально, что выгодно отличает критерий от алгебраических КУ. КУ Найквиста имеет ясный физический смысл: связь стационарных частотных свойств разомкнутой САУ с нестационарными свойствами замкнутой САУ. По Найквисту, для устойчивости САУ необходимо и достаточно чтобы ее АФЧХ не охватывала критическую точку (-1;0) при изменении частоты от 0 до ∞.

В соответствии с критерием Найквиста АФЧХ синтезированной системы не охватывает выше упомянутую критическую точку – поэтому является устойчивой, при этом запас по амплитуде ΔL=∞, а по фазе Δφ≈920. Запас устойчивости необходим, для того чтобы система оставалась устойчивой при перегрузках.

ЛЧХ (рисунок 10) служат для определения устойчивости системы по взаиморасположению ЛАЧХ и ЛФЧХ. Если частота среза ЛАЧХ расположена правее точки в которой ЛФЧХ достигает угла в -1800 то система устойчива.

Литература

1.Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп; пер. с англ. Б.И. Копылова. - М.: Лаборатория Базовых Знаний, 2002. - 832 с.

2.Грачева, Л.Н. Экспериментальное построение переходной характеристики ТП полимеризации лонжерона лопасти : материалы республиканской научно-практической конференции «Инновационные процессы в системе непрерывного образования в целях кадрового обеспечения предприятий южного региона республики Башкортостан» / Л.Н.Грачева, Н.И.Тюков, Е.А. Закурдаева. – Уфа: РИОРУНМЦ МО РБ, - 2004.- С. 121-128.

3.Ерофеев, А.А. Теория автоматического управления: учебник для вузов / А.А. Ерофеев. - СПб.: Политехника, 2003. - 302 с.

4.Первушин, Ю.С. Композиционные материалы: учебное пособие по дисциплине: «Технология композиционных материалов». - Уфа:УГИС, 2005.-с

5.Галлиев А. Л., Галиева Р. Г. Элементы и устройства автоматизированных систем управления: Учеб.посоие. – Стерлитамак: Стерлитамак. Гос .пед .акад., 2007. – 220 с.

Приложение

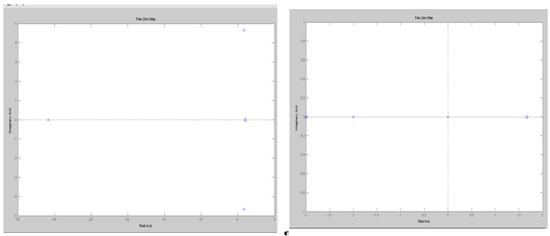
Рисунок 8 -Положение корней и нулей системы замкнутой и разомкнутой

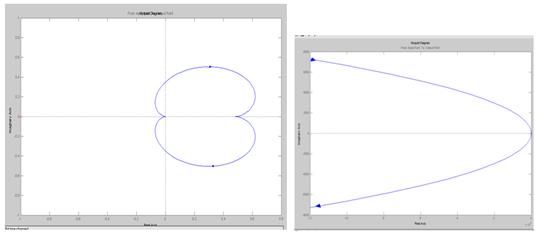
Рисунок 9 –Критерий Найквиста замкнутой и разомкнутой систем

технический проект композиционный материал

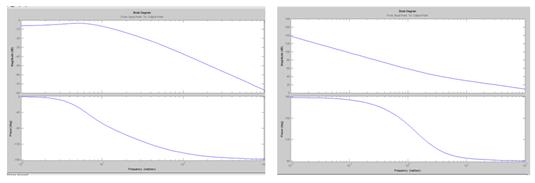
Рисунок 10 – логарифмические АЧХ и ФЧХ системы замкнутой и разомкнутой

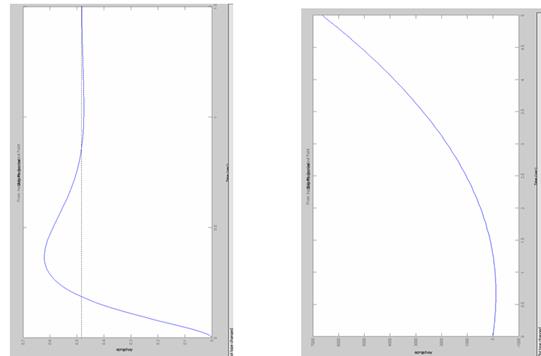
Рисунок 11 - Переходная характеристика замкнутой и разомкнутой систем