Курсовая работа: Полунормальные подгруппы конечной группы

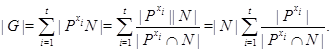
Положим . Элемент можно выбрать единичным, поэтому и . Теперь

Проверим, что под знаком суммы нет слагаемых равных 1. Допустим противное, т.е. что для некоторого имеем равенство . Это означает, что и подгруппа содержит две подгруппы и порядка . По существует элемент такой, что . Но тогда , а так как , то и . Но это возможно только при , противоречие. Значит, допущение неверно и в равенстве <6> под знаком суммы все слагаемые отличны от единицы. Поскольку каждое слагаемое есть степень простого , то из равенства <6> получаем сравнение . По все подгруппы порядка группы сопряжены между собой, а число подгрупп сопряжённых с равно . Поскольку , то делит .

Теорема доказана.

Силовской – подгруппой конечной группы называют такую – подгруппу, индекс которой не делится на . Непосредственно из теоремы получаем

Следствие 1.4 Пусть конечная группа имеет порядок , где – простое число и не делит . Тогда:

существует силовская –подгруппа и её порядок равен ;

каждая –подгруппа содержится в некоторой силовской –подгруппе;

любые две силовские –подгруппы сопряжены;

число силовских –подгрупп сравнимо с единицей по модулю и делит .

Теорема 1.5 Для конечной группы и её силовской –подгруппы справедливы следующие утверждения:

если , то – силовская –подгруппа в , а – силовская –подгрупппа в ;

;

если и , то

и

пусть – все простые делители порядка группы , при , и пусть – соответствующие им силовские подгруппы. Тогда

а если , то .

Д о к а з а т.е. л ь с т в о. Так как и не делит , то – –группа, а из того, что

следует

и не делится на . Значит – силовская –подгруппа в .

Поскольку , то – –группа, а так как