Курсовая работа: Понятие состояния квантово-механической системы. Принцип суперпозиции

.

Используя соотношение (2.1.1) запишем это равенство в интегральной форме

(2.1.2)

или с помощью скобок

(2.1.2а)

Операторы, для которых выполняется это соотношение, считаются самосопряженными (эрмитовыми). Дадим общее определение такого оператора.

Каждому оператору можно привести в соответствие другие: комплексно сопряженный с ним , транспонированный , сопряженный .

Оператор является комплексно сопряженным с оператором , если выполняется соотношение: .

Операторы и называют транспонированными друг с другом, если выполняется соотношение

(2.1.3)

или в скобочной форме

. (2.1.3а)

Оператор называют сопряженным оператору . Следовательно, для произвольной пары функций и и операторов и имеет место соотношение

(2.1.4)

или в интегральной форме

. (2.1.4а)

Самосопряженным называется оператор, если он равен своему сопряженному: =.

Из соотношения (2.1.4) следует, что для самосопряженного оператора и произвольной пары функций и должно выполняться равенство:

(2.1.5)

или

(2.1.5а)

Пример.Найти оператор, сопряженный с. Является ли этот оператор самосопряженным?

Подставим оператор в левую часть равенства (2.1.4а) и проинтегрируем полученный интеграл по частям:

.

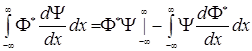Так как ,имеем

.

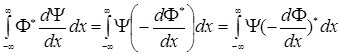Сравнивая это соотношение с (2.1.4а), получаем . В данном случае , поэтому оператор не является самосопряженным.

2.2 Алгебраические действия с операторами

Имея в распоряжении несколько простых операторов можно получить из них более сложные.