Курсовая работа: Понятие состояния квантово-механической системы. Принцип суперпозиции
![]() .
.
Символически это записывается так:
![]() .
.
Например, ![]()
Произведением операторов ![]() и
и ![]() будем называть оператор
будем называть оператор ![]() , который определяется следующим образом:
, который определяется следующим образом:
![]() ,
,
причем на функцию сначала действуем ближайшим к ней оператором, а потом на полученный результат – следующим,
![]() .
.
Символически произведение операторов записывается в виде ![]() .
.
Например, ![]() . Подействуем произведением этих операторов на функцию
. Подействуем произведением этих операторов на функцию ![]() :
:
![]() .
.
Если действие одного и того же оператора повторяется n раз, это записывается в виде степени этого оператора:
![]() .
.
Например,
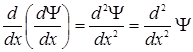 .
.
Произведение операторов зависит от порядка множителей. Например, если ![]() , то
, то 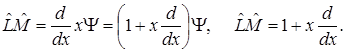 Но
Но ![]() . Очевидно, что в этом случае
. Очевидно, что в этом случае ![]() . Таким образом, операторы, вообще говоря, являются некоммутативными (неперестоновочными). Если
. Таким образом, операторы, вообще говоря, являются некоммутативными (неперестоновочными). Если ![]() , то операторы называют комутирующими. В этом случае
, то операторы называют комутирующими. В этом случае ![]() . Выражение
. Выражение ![]() называют коммутатором.
называют коммутатором.
2.3 Собственные функции и собственные значения оператора
В результате действия оператора ![]() на функцию
на функцию ![]() иногда получается та же самая функция, умноженная на некоторое число а:
иногда получается та же самая функция, умноженная на некоторое число а:
![]() (2.3.1)
(2.3.1)
Например, 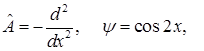
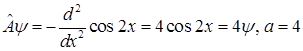 .
.
Если имеет место уравнение (2.3.1) и функции ![]() удовлетворяют стандартным условиям (конечность, непрерывность, однозначность), то
удовлетворяют стандартным условиям (конечность, непрерывность, однозначность), то ![]() называют собственной функцией оператора
называют собственной функцией оператора ![]() , а число
, а число ![]() – его собственным значением, соответствующим данной собственной функции
– его собственным значением, соответствующим данной собственной функции ![]() . Соотношение (2.3.1) называют уравнением собственных значений оператора. Совокупность чисел
. Соотношение (2.3.1) называют уравнением собственных значений оператора. Совокупность чисел ![]() , при которых это уравнение имеет решение, удовлетворяющее стандартным условиям, называют спектром собственных значений оператора. Спектр собственных значений может быть как дискретным, так и непрерывным множеством. Если спектр собственных значений дискретный, то собственные функции и собственные значения нумеруют:
, при которых это уравнение имеет решение, удовлетворяющее стандартным условиям, называют спектром собственных значений оператора. Спектр собственных значений может быть как дискретным, так и непрерывным множеством. Если спектр собственных значений дискретный, то собственные функции и собственные значения нумеруют:
![]()
![]()
![]() , n= 1, 2, 3,…
, n= 1, 2, 3,…
Число n называют квантовым.
Иногда одному и тому же собственному значению соответствует несколько собственных функций. В таком случае говорят, что собственное значение является вырожденным. Число разных функций, принадлежащих одному и тому же собственному значению, называют кратностью вырождения.
Перейдем к физической интерпретации рассмотренных выше математических понятий. Отклонение физической величины A от ее среднего значения ![]() есть:
есть: ![]() . Введем оператор, соответствующий этой величине:
. Введем оператор, соответствующий этой величине: ![]() . Тогда по формуле (2.1.1) можно найти среднее квадратичное отклонение физической величины от ее среднего значения в состоянии
. Тогда по формуле (2.1.1) можно найти среднее квадратичное отклонение физической величины от ее среднего значения в состоянии ![]() :
:
![]() .
.