>> w= TF([1,36,9],[1,15,18,34])

Transfer function:

s^2 + 36 s + 9

------------------------

s^3 + 15 s^2 + 18 s + 34

>>pole(w)

ans =

-13.8796

-0.5602 + 1.4614i

-0.5602 - 1.4614i

>>zero(w)

ans =

-35.7482

-0.2518

>>step(w)

>>impulse(w)

>>bode(w)

>>nyquist(w)

>>ltiview(w)

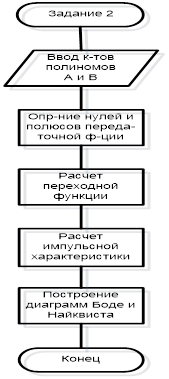
Рисунок 2.6 – Блок-схема программы исследования характеристик динамической системы

Задание 3. Построение модели с распределенными параметрами

3.1 Постановка задачи

Применение метода конечных разностей для расчета теплового режима твердой стенки

Плоская стенка первоначально прогрета равномерно до температуры 600С. В дальнейшем на внутренней поверхности стенки (х = 0) обеспечивается условие теплоизоляции (плотность теплового потока равна нулю), а с наружной поверхности (х = L) идет теплообмен с внешней средой, имеющей постоянную температуру Тср = -40 0С.. Изменение температуры в стенке осуществляется в результате процесса теплопроводности. Требуется получить зависимость от времени температуры на внутренней поверхности стенки. Толщина стенки L=20смб коэффициент теплоотдачи α=100Вт/м2К (неявная схема).

3.2 Математическая постановка задачи

Для неявной разностной схемы апроксимация уравнения теплопроводности будет иметь следующий вид:

(3.1)

Теперь удобно ввести и в левой и правой части сгруппировать все члены с индексрмj+1:

(3.2)