Курсовая работа: Построение математических моделей методом идентификации

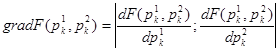(4.4)

Направление вектора градиента совпадает с направлением наискорейшего возрастания функции F(p¹ ,p² ). Вектор − gradF(p¹ ,p² ) называется антиградиентом, его направление совпадает с направлением наискорейшего убывания функции. Предполагается, что компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью вычислены при помощи численных методов.

Выбор величины шага λ осуществляется путем решения задачи минимизации F(p¹ ,p² ) в направленииgradF(p¹ ,p² ) с помощью одного из методов одномерного поиска.

Преимущество метода в том, что при переходе от шага к шагу обеспечивается выполнение неравенстваF(p¹ _{k +1} ,p² _{k +1} )<= F(p¹ _k ,p² _k ), т.е. значение функции цели улучшается.

Скорость сходимости метода при решении некоторых задач является недопустимо низкой.

Это связано с тем, что изменения переменных непосредственно зависят от величины градиента, которая стремится к нулю в окрестности точки минимума. Поэтому метод наискорейшего спуска эффективен при поиске на значительных расстояниях от точки минимума x* и плохо работает в окрестности этой точки.

4.3 Описание входных и выходных переменных

В качестве входных переменных имеем массив независимых значений Х и фактические значения отклика YF, точность вичислений eps.

Выходные величины – конечне значения p¹ и p² , при которых достигается минимум функции F(p¹ ,p² ), количество итераций, что характеризует скорость сходимости метода и значение функции F(p¹ ,p² ), а также график сравнения фактического и расчетного значения отклика и таблицу с фактическим и расчетным значениями отклика.

4.4 Текст программы в SciLab

//Входные данные

X1=[1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6];

YF=[20 30 70 85 100 90 100 108 120 110 124]; //Y фактическое

//Расчетная функции в виде у=р1-р2expХ1)

function YR=raschet(P)

YR=P(1)-P(2)*exp(-X1);

endfunction

//Минимизируемая функция как результат

//ошибки расчетных и фактических значений

function F=oshibka(P)

F=sum((YF-raschet(P))^2);

endfunction

eps=0.00001; //точность вычислений

P=[10 0.9]; //начальное приближение

lamda=1; //параметр,характеризующий длину шага

F0=oshibka(P*2);

F=oshibka(P);

i=0;

while abs(F0-F)>eps