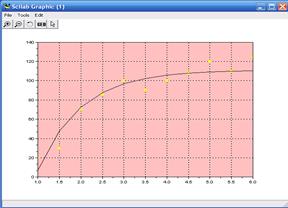
1. 20. 7.0019302 168.94982

1.5 30. 47.886197 319.91604

2. 70. 72.683758 7.2025575

2.5 85. 87.724239 7.4214795

3. 100. 96.846752 9.9429717

3.5 90. 102.37984 153.26034

4. 100. 105.73582 32.899642

4.5 108. 107.77133 0.0522905

5. 120. 109.00593 120.86965

5.5 110. 109.75475 0.0601485

6. 124. 110.20893 190.19358

Среднее квадратическое отклонениеsigma = 1010.7685

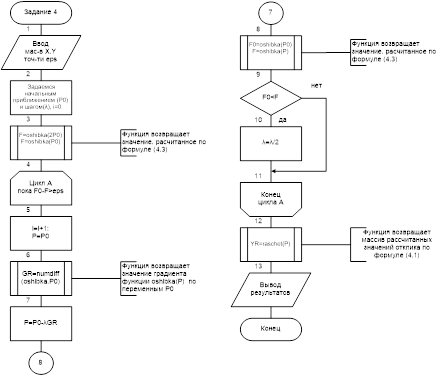
4.6 Блок-схема программы

Задание 5. Разработка аналитических моделей объектов автоматизации. Линеаризация моделей

5.1 Постановка задачи

Разработайте математическую модель заданной динамической системы. Построить аналитическую модель емкости с одним притоком и двумя стоками (например двухручьевая МНЛЗ) и провести ее линеаризацию. Математическую модель заданного объекта представить в виде программы на ЭВМ, рассчитать кривые исходной и линеаризованной модели отклика модели на ступенчатое и импульсное воздействие. Предложить методику идентификации параметров модели. Какие эксперименты будет необходимо провести на реальном объекте? Оцените необходимый объем и форму представления результатов.

5.2 Математическая постановка задачи

В данном объекте управления выходной величиной является уровень металла в промежуточном ковше h, а входной величиной – разность между притоком и стоками металла ∆G=G_пр -G_ст1 -G_ст2 , причем возмущения могут возникать за счет изменения G_пр ,G_ст1 и G_ст2 .

Изменение уровня характеризуется следующим дифференциальным уравнением:

, (5.1)

где ρ – плотность металла, F – площадьзеркала металла в промковше.

Известно, что сток жидкости через отверстие пропорционален корню квадратному из высоты этой жидкости на отверстием:

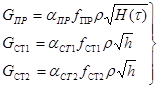(5.2)

где α_пр ,α_ст1 ,α_ст2 – коэффициенты расхода на притоке и стоках; f_пр ,f_ст1 ,f_ст2 – проходные сечения в стопорных парах или в шиберных затворах сталеразливочного и промежуточного ковшей; H(t) – текущее значение уровня металла в сталеразливочном ковше.

С использование зависимостей (5.2) уравнение (5.1) приобретает вид нелинейного дифференциального уравнения первого порядка:

(5.3)

Уравнение можно несколь?