Курсовая работа: Построение математических моделей методом идентификации

Так как в задаче заданна температура окружающей среды, то имеем граничные условия 3-го рода. Запишем уравнения для граничных и внутренних точек одного временного слоя.

Для i=1, имеем:

(3.3)

(3.4)

Обозначим , , получим уравнение для i=1:

(3.5)

Для i=2…n-1, имеем:

(3.6)

(3.7)

(3.8)

Для i=n, имеем:

(3.9)

(3.10)

Обозначим , , получим уравнение для n=1:

(3.11)

Рассмотрим метод прогонки для решения системы, сотоящей из уравнений (3.5), (3.8), (3.11). Из уравнения (3.5) выразим U_{1, j +1} :

(3.12)

, (3.13)

Запишем уравнение для i=2 (3.8) и подставим в него выражение (3.12) и выразим U_{2, j +1} :

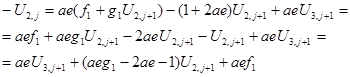(3.14)

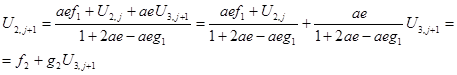(3.15)

(3.16)

Продолжим этот процесс до i=n-1, получим:

(3.17)

Коэффициенты f_i и g_i известны из граничных условий на первой границе f₁ =U_{1, j} и g_i =0, их называют прогоночными коэффициентами, и мы можем их найти по возрастающей рекурсии вплоть до i=n-1. Можем записать:

(3.18)

Подставим выражение (3.18) в уравнение для второй границы (3.11) и выразим U_{n , j +1} :

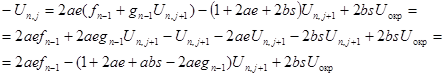(3.19)

(3.20)