Курсовая работа: Построение математической модели оптимального управления обеспечивающего мягкую посадку при

кг/с.

Наш критерий оптимизации . Введем принятые в исходных данных обозначения:

; .

Начальный момент времени t=0, конечный момент времени – момент посадки КА (момент столкновения с планетой) t=T.

;

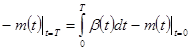Тогда критерий оптимизации:

;

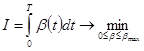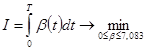. (Здесь .)

Теперь необходимо написать уравнение состояния системы. Для этого нужно ввести переменные состояния и входную переменную.

Порядок дифференциального уравнения n=3, отсюда 3 уравнения состояния:

;

;

.

Выберем управление:

;

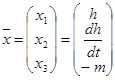
Подставляем уравнения состояния, получим:

так как и , отсюда

;

;

.

Критерий оптимизации:

.

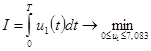Введем переменные х₀ и х_n+1 (то есть х₄ ).

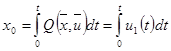, где t – текущее время.

.

Тогда основные уравнения состояния: