Курсовая работа: Представление функции рядом Фурье

Рассмотрим систему функций , определенных в промежутке [a, b] и непрерывных или кусочно-непрерывных. Если все функции данной системы попарно ортогональны, то есть

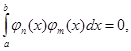
то ее называют ортогональной системой функций. При этом всегда будем полагать, что

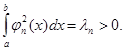
Если , то система называется нормальной. Если же это условие не выполняется, то можно перейти к системе 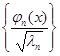, которая уже заведомо будет нормальной.

Важнейшим примером ортогональной системы функций как раз и является тригонометрическая система

(10)

в промежутке , которую мы рассматривали ранее. Ее ортогональность следует из соотношений (5), (7), (8). Однако она не будет нормальной ввиду (9). Умножая тригонометрические функции (10) на надлежащие множители, легко получить нормальную систему:

(10*)

Пусть в промежутке дана какая-нибудь ортогональная система функций . Зададимся целью разложить определенную в функцию в «ряд по функциям » вида:

(11)

Для определения коэффициентов данного разложения поступим так же, как мы это сделали в предыдущем параграфе, а именно умножим обе части равенства на и проинтегрируем его почленно:

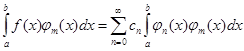
В силу ортогональности системы, все интегралы справа, кроме одного, будут равны нулю, и легко получается:

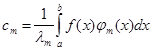(m=0, 1, 2, …) (12)

Ряд (11) с коэффициентами, составленными по формулам (12), называется обобщенным рядом Фурье данной функции, а сами коэффициенты—ее обобщенными коэффициентами Фурье относительно системы . В случаи нормальной системы функций коэффициенты будут определяться следующим образом:

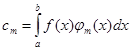
В данном случаи все замечания сделанные в предыдущем параграфе необходимо повторить. Обобщенный ряд Фурье, построенный для функции , связан с ней лишь формально и в общем случае эту связь обозначают следующим образом:

Сходимость этого ряда, как и в случае тригонометрического ряда, подлежит еще исследованию.

Интеграл Дирихле Принцип локализации

Пусть будет непрерывная или кусочно-непрерывная функция с периодом . Вычислим постоянные (ее коэффициенты Фурье):

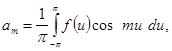
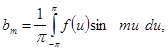
и по ним составим ряд Фурье нашей функции

Как видим, здесь коэффициент мы определили по общей формуле для при , но зато свободный член ряда запишем в виде .

Если функция F(x) кусочно-непрерывна в любом конечном промежутке и к тому же имеет период , то величина интеграла

по прежнему промежутку длины не зависит от .