Курсовая работа: Представление функции рядом Фурье

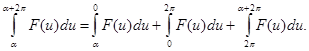
Если в последнем интеграла сделать подстановку , то он приведется к интегралу

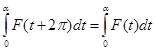
и лишь знаком будет отличаться от первого интеграла. Таким образом, рассматриваемый интеграл оказывается равным интегралу

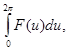
уже не содержащему .

Для того чтобы исследовать поведение ряда в какой-нибудь определенной точке , составим удобное выражение для его частичной суммы

Подставим вместо и их интегральные выражения и подведем постоянные числа под знак интеграла:

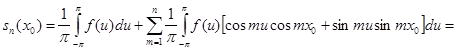
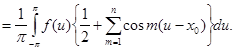
Легко проверить тождество

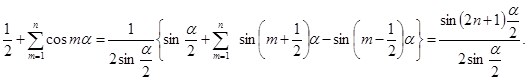
Воспользуемся этим тождеством для преобразования подынтегрального выражения, окончательно получим

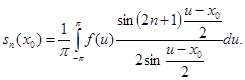(13)

Этот интеграл называют интегралом Дирихле, хотя у Фурье он встречается гораздо раньше.

Так как мы имеем дело с функцией от u периода , то промежуток интегрирования по сделанному выше замечанию можно заменить, например, промежутком

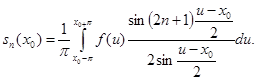
Подстановкой преобразуем этот интеграл к виду

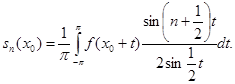
Затем, разбивая интеграл на два: и приводя второй интеграл путем замены знака переменной тоже к промежутку , придем к такому окончательному выражению для частичной суммы ряда Фурье:

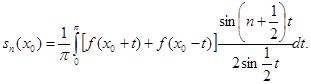(14)

Таким образом, дело сводится к исследованию поведения именно этого интеграла, содержащего параметр n.

Для дальнейшего изложения материала нам потребуется одна лемма, принадлежащая Риману, которую мы оставим без доказательства.

Если функция непрерывна или кусочно-непрерывна в некотором конечном промежутке , то

и, аналогично,

Если вспомнить формулы, выражающие коэффициенты Фурье , то в качестве первого непосредственного следствия из леммы получается утверждение: