Курсовая работа: Представление функции рядом Фурье

В отношении концов промежутка сохраняют силу замечания, сделанные в предыдущем параграфе относительно точек Конечно, промежуток может быть заменен любым другим промежутком длинны в частности, промежутком . В последнем случае формулы (20) должны быть заменены формулами

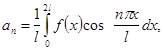
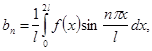(20a)

Случай четных и нечетных функций

Если заданная в промежутке функция будет нечетной, то очевидно

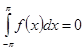
В этом легко убедится:

.

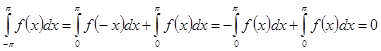Таким же путем устанавливается, что в случае четной функции :

.

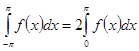Пусть теперь будет кусочно-дифференцируемая в промежутке четная функция. Тогда произведение окажется нечетной функцией, и по сказанному

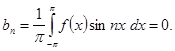
Таким образом, ряд Фурье четной функции содержит одни лишь косинусы:

(21)

Так как в этом случае будет тоже четной функцией, то, применив сюда второе из сделанных выше замечаний, можем коэффициенты разложения написать в виде

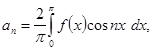
(22)

Если же функция будет нечетной, то нечетной будет и функция , так что

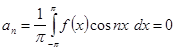
Мы приходим к заключению, что ряд Фурье нечетной функции содержит одни лишь синусы:

(23)

При этом ввиду четности произведения можно писать:

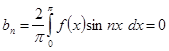
(24)

Отметим, что каждая функция , заданная в промежутке , может быть представлена в виде суммы четной и нечетной составляющих функций:

,

Где

Очевидно, что ряд Фурье функции как раз и составится из разложения по косинусам функции и разложения по синусам функции .

Предположим, далее, что функция задана лишь в промежутке . Желая разложить ее в этом промежутке в ряд Фурье мы дополним определение нашей функции для значений x в промежутке по произволу, но с сохранением кусочной дифференцируемости, а затем применим сказанное в пункте «Случай непериодической функции».

Можно использовать произвол в определении функции в промежутке так, что бы получить для разложение только лишь по косинусам или только по синусам. Действительно, представим семе, что для мы полагаем , так что в результате получается четная функция в промежутке . Ее разложение, как мы видели, будет содержать одни лишь косинусы. Коэффициенты разложения можно вычислять по формулам (22), куда входят лишь значения первоначально заданной функции .