Курсовая работа: Представление функции рядом Фурье

стремится к пределу , а — к нулю. Если же есть «точка стыка», то при этом она может оказаться как точкой непрерывности, так и точкой разрыва. В первом случае мы опять столкнемся с отношением (17), но они будут стремиться на этот раз к различным пределам, соответственно—к производной справа и к производной слева. К аналогичному результату придем и в случае разрыва, но здесь заменится значениями тех функций, от склеивания которых получилась данная, а пределами отношений (17) будут односторонние производные упомянутых функций при .

Итак, наше заключение справедливо во всех случаях.

Случай непериодической функции

Вся построенная выше теория исходила из предположения, что заданная функция определена для всех вещественных значений x и притом имеет период . Между тем чаще всего приходится иметь дело с непериодической функцией f(x), иной раз даже заданной только в промежутке .

Что бы иметь право применить к такой функции изложенную теорию, введем взамен нее вспомогательную функцию определенную следующим образом. В промежутке мы отождествляем с f(x):

(18)

затем полагаем

а на остальные вещественные значения x распространяем функцию по закону периодичности.

К построенной таким образом функции с периодом можно уже применить доказанную теорему разложения. Однако, если речь идет о точке , строго лежащей между и , то, ввиду (18), нам пришлось бы иметь дело с заданной функцией . По той же причине и коэффициенты разложения можно вычислить по формулам вычисления коэффициентов не переходя к вспомогательной функции. Короче говоря, все доказанное выше непосредственно переносится на заданную функцию , минуя вспомогательную функцию .

Особого внимания, однако, требуют концы промежутка . При применении к функции теоремы предыдущего параграфа, скажем, в точке , нам пришлось бы иметь дело как со значениями вспомогательной функции справа от , где они совпадают уже со значениями справа от ю Поэтому для в качестве значения надлежало бы взять

.

Таким образом, если заданная функция даже непрерывна при , но не имеет периода , так что , то—при соблюдении требований кусочной дифференцируемости—суммой ряда Фурье будет число

отличное как от , так и от . Для такой функции разложение имеет место лишь в открытом промежутке .

Следующее замечание так же заслуживает особого внимания. Если тригонометрический ряд

сходится в промежутке к функции , то ввиду того, что его члены имеют период , он сходится всюду, и сумма его тоже оказывается периодической функцией с периодом . Но эта сумма вне указанного промежутка вообще уже не совпадает с функцией .

Случай произвольного промежутка

Предположим, что функция задана в промежутке произвольной длины и кусочно-дифференцируема в нем. Если прибегнуть к подстановке

,

то получится функция от в промежутке , тоже кусочно-дифференцируемая, к которой уже приложим рассмотрения предыдущего параграфа. Как мы видели, за исключением точек разрыва и концов промежутка, можно разложить ее в ряд Фурье:

коэффициенты которого определяются формулами Эйлера—Фурье:

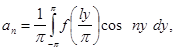
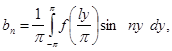
вернемся теперь к прежней переменной , полагая

.

Тогда получим разложение заданной функции в тригонометрический ряд несколько измененного вида:

(19)

Здесь косинусы и синусы берутся от углов, кратных не , а . Можно было бы и формулы для определения коэффициентов разложения преобразовать той же подстановкой к виду