Курсовая работа: Представления конечных групп

Такое отображение является точным представлением группы .

1.4. Пусть –конечная группа, состоящая из элементов и пусть – симметрическая группа на . Отображение, которое ставит в соответствие элементу подстановку

является инъективным гомоморфизмом группы в . С такой подстановкой мы свяжем матрицу

где, как и в примере ,

Тогда отображение является точным представлением группы . Оно называется правым регулярным представлением этой группы. Определим следующим образом:

Тогда

и, если , то каждый диагональный элемент равен нулю.

регулярное представление группы определяется аналогично с использованием гомоморфизма

Другими словами,

Пусть – некоторый гомоморфизм из в , т.е. подстановочное представление группы . Представив подстановку в виде матрицы , как это сделано в примере 1.3, мы получим представление

Пусть – представление степени . Говорят, что приводимо, если существует такая невырожденная матрица , что

где и – квадратные матрицы порядка и соответственно, причем Отметим, что представления

эквивалентны, поскольку для матрицы

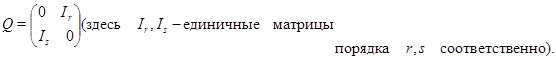
Скажем, что представление неприводимо, если оно не является приводимым. Отметим, что в (1.3) отображения и являются представлении степеней и соответственно.

Для заданных представлений и группы степеней и соответственно отображение

является представление степени этой группы. Такое, представление называется прямой суммой представлений и и обозначается через .