Курсовая работа: Представления конечных групп
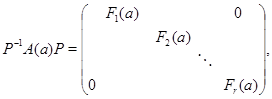
где каждое ![]() является неприводимым представлением группы
является неприводимым представлением группы ![]() .
.
1.2 Представления унитарными матрицами и полная приводимость представлений конечных групп
Представление ![]() группы
группы ![]() называется унитарным, если для всех
называется унитарным, если для всех ![]() матрица
матрица ![]() является унитарной, т.е.
является унитарной, т.е. ![]() . Здесь
. Здесь ![]() обозначает матрицу, транспонированную к
обозначает матрицу, транспонированную к ![]() , где
, где ![]() , а
, а ![]() – величина, комплексно – сопряженная к
– величина, комплексно – сопряженная к ![]() . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
. В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
Матрица ![]() называется эрмитовой, если
называется эрмитовой, если ![]() , и положительно определенной, если
, и положительно определенной, если ![]() для каждого ненулевого столбца
для каждого ненулевого столбца ![]() . Следующая лемма тривиальна.
. Следующая лемма тривиальна.
Лемма 2.1. Пусть ![]() – произвольная невырожденная матрица. Тогда
– произвольная невырожденная матрица. Тогда ![]() – положительно определенная эрмитова матрица. Кроме того, сумма положительно определенных эрмитовых матриц также является положительно определенной эрмитовой матрицей.
– положительно определенная эрмитова матрица. Кроме того, сумма положительно определенных эрмитовых матриц также является положительно определенной эрмитовой матрицей.
Лемма 2.2. Для любой положительно определенной эрмитовой матрицы ![]() найдется невырожденная верхнетреугольная матрица
найдется невырожденная верхнетреугольная матрица ![]() , такая, что
, такая, что ![]() .
.
Доказательство. Пусть ![]() . Тогда
. Тогда ![]() и
и ![]() . Пусть
. Пусть
![]() .
.
Положим
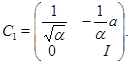
Тогда
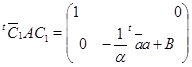
и ![]() – положительно определенная эрмитова матрица. Для завершения доказательства достаточно воспользоваться индукцией по порядку матрицы
– положительно определенная эрмитова матрица. Для завершения доказательства достаточно воспользоваться индукцией по порядку матрицы ![]() .
.
Теорема 2.3. Пусть ![]() – конечная группа. Для каждого представления
– конечная группа. Для каждого представления ![]() группы
группы ![]() найдется невырожденная верхнетреугольная матрица
найдется невырожденная верхнетреугольная матрица ![]() , такая, что
, такая, что ![]() является унитарной матрицей для всех
является унитарной матрицей для всех ![]() .
.
Доказательство. Положим
![]()
Тогда в силу леммы 2.1 ![]() является положительно определенной эрмитовой матрицей. Таким образом, найдется невырожденная верхнетреугольная матрица
является положительно определенной эрмитовой матрицей. Таким образом, найдется невырожденная верхнетреугольная матрица ![]() , такая, что
, такая, что ![]() и поэтому
и поэтому ![]() . Так как
. Так как
![]()
то ![]() , т.е.
, т.е. ![]() ; поэтому
; поэтому ![]() – унитарная матрица.
– унитарная матрица.
Теорема 2.4. Каждое представление конечной группы вполне приводимо.
Доказательство. Пусть ![]() – приводимое представление конечной группы
– приводимое представление конечной группы ![]() , и пусть
, и пусть ![]() разлагается следующим образом:
разлагается следующим образом:

В силу предыдущей теоремы существует невырожденная матрица ![]() , такая, что
, такая, что ![]() – унитарная матрица. Так как
– унитарная матрица. Так как ![]() верхнетреугольная, то
верхнетреугольная, то ![]() имеет вид
имеет вид

Поскольку ![]() , мы получаем
, мы получаем

откуда следует, что ![]() .
.
1.3 Лемма Шура
Лемма 3.1. (Лемма Шура.) Пусть ![]() и
и ![]() – неприводимые представления группы
– неприводимые представления группы ![]() степеней
степеней ![]() и
и ![]() соответсвенно. Пусть
соответсвенно. Пусть ![]() – такая
– такая ![]() – матрица, что
– матрица, что