Курсовая работа: Приближённые методы решения алгебраического уравнения

Аналогично находим

n=1, 2, … (4.8)

Покажем, что последовательность {x_n } стремится к корню уравнения (1.0) монотонно.

Предположим для определённости, что f ¢(x) и f ¢¢(x) >0, a<x<b (рис 1.8). В этом случае функция f(x) строго монотонна и строго выпукла вниз. Следовательно, любая внутренняя точка хорды, соединяющей крайние точки графика функции f(x), лежит над соответствующей точкой графика функции f(x), т. е.

l(x) > f(x), a > x > b

В частности, если х₀ корень уравнения (1.1): f(x₀ ) = 0, отсюда следует, что

l(x₀ ) > 0

C (3.8) и (4.8) получаем:

l(x) = 0, a > x₁ > b

Таким образом,

l(x₁ ) < l(x₀ ) (5.8)

но линейная функция l(x) строго монотонно возрастает, так как

l(b) = f(b) > f(a) = l(a)

поэтому из (5.8) следует x₁ < x₀ , заменяя теперь отрезок [a, b] отрезком [x₁ , b] и замечая, что f(x₁ ) < 0 , аналогично можно доказать, что x₁ < x₂ < x₀ , далее по индукции получим:

x₁ < x₂ < … < x_n < … < x₀ ,

Таким образом, последовательность {x_n }, будучи монотонной, сходится. Пусть lim x_n = c, при n®¥ . Переходя к пределу при n®¥ в равенстве (4.8) получим f(c)=0, т. е. последовательность {x_n } сходится к корню уравнения (1.1).

Если | f ¢(x)|³m>0, a<x<b, то не трудно получить оценку погрешности сходимости последовательности {x_n } через значения самой функции f(x) в точках x_n . Действительно,

f(x_n )= f(x_n )- f(x₀ )= f ¢(x_n )×(x_n -x₀ ),

x_n <x_n <x₀ , n = 1, 2, …,

Отсюда:

, n = 1, 2, …,

Остальные случаи, т. е. случаи:

,

,

рассматриваются аналогично разобранному (рис 2.8).

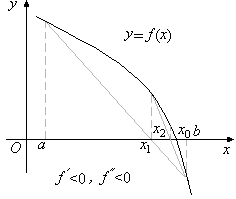
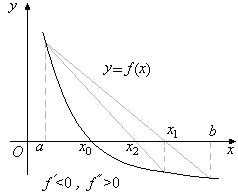
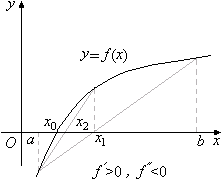
рис. 2.8