Курсовая работа: Применение методов моделирования к электротехническим задачам

L₁ = a₁₂ ∙ a₂₁ =(0,22+0,032j)·(0,535-0,01j)=0,118+0,015j;

L₂ = a₂₃ ∙ a₃₂ =(0,464+0,0023j)·(0,061+0,011j)=0,028+0,00065j.

Тогда находим оставшиеся члены формулы

Δ_н =1- (L₁ +L₂ )=1- (0,118+0,015j + 0,028+0,00065j) =0,854-0,016j;

P_{5321 н} =a₅₃ ·a₃₂ ·a₂₁ =(0,143-2,39j)∙(0,464+0,0023j)·(0,22+0,032j)=

= 0,051-0,242j.

Алгебраические дополнения путей вычисляются следующим образом

Δm_41н =1- (L₂ )=1-0,028-0,00065j =0,972-0,00065j;

Δm_61н =1- (L₂ )= 1-0,028-0,00065j =0,972-0,00065j;

Δm_5321н =1;

Δm_7321н =1.

Вычисляем напряжение в первом узле по формулам (5.1), приведенным выше

.

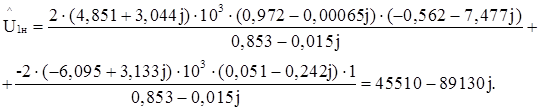
Погрешность равна

;

.

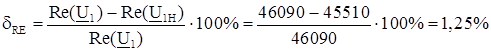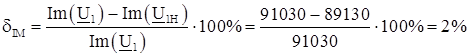Как видим, погрешности меньше 5%, следовательно, расчеты верны. Напряжение в узлах, найденное с использованием формулы Мэзона, получилось одинаковым для ненормализованного и нормализованного графа, следовательно, эти графы равносильны.

6 ПОСТРОЕНИЕ НЕНОРМАЛИЗОВАННОГО U-ГРАФА ПРЯМЫМ МЕТОДОМ

Алгоритм построения U-графа прямым методом следующий:

1. На поле графа наносим узлы, которые соответствуют неизвестным напряжениям в узлах схемы;

2. Каждую пару узлов соединяем двумя противоположно направленными ветвями с передачами равными взаимным проводимостям между узлами схемы и помноженными на -1;

3. Строим в узлах графа петли с передачами равными сумме проводимостей всех ветвей, сходящихся в данном узле и прибавляем к ним единицу;

4. Наносим на поле графа узлы-источники и соединяем их с зависимыми узлами передачами равными -1, если ток подтекает к узлу, и +1, в противоположном случае.

Пользуемся схемой, представленной в каноническом виде (рисунок 3.1). В результате получаем граф, изображенный на рисунке 6.1. Находим значения проводимостей

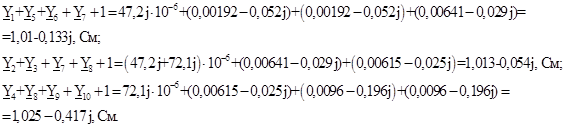
В результате получили ненормализованный граф, изображенный на рисунке 6.2. Ненормализованные U-графы, построенные прямым и косвенным методом, получились одинаковыми, что говорит об их равносильности.

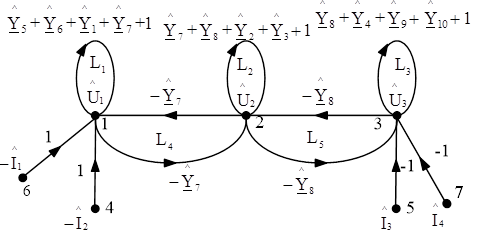
Рисунок 6.1 – Ненормализованный U–граф, построенный прямым методом