Курсовая работа: Прогнозирование емкости и коньюктуры рынка
где tg – табличное значение по распределению Стьюдента с числом степеней свободы
К = n – 1 и уровнем значимости а; ![]() – дисперсия временного ряда.
– дисперсия временного ряда.
| S(yt – | = | 14,6 | = 1,46 | |
| n | 10 |
При заданном уровне значимости a = 0,05 (g = 1 – а = 1 – 0,05 = 0,95) и числе степеней свободы К = 10 – 1 = 9, определим табличное значение t-критерия Стьюдента (см. Приложение 1). Табличное значение критерия Стьюдента tg = 2,262.
Определим интервальный прогноз.
![]() =17,7 – 2,262 ×
=17,7 – 2,262 ×![]() = + 14,8
= + 14,8
![]() =24,16 + 2,262 ×
=24,16 + 2,262 ×![]() = + 20,6
= + 20,6
Таким образом, с вероятностью 0,95 (95%) можно говорить о том, что на 11-ю неделю уровень ряда будет находиться в промежутке между 14,8 и 20,6.
Задание № 2
| Период | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Уровень ряда | 11,0 | 10,8 | 10,7 | 10,5 | 11,7 | 12,2 | 12,5 | 12,1 | 13,0 | 13,7 | 13,0 | 14,0 |
По данным о ежедневном обороте магазина «Ткани для дома»:
1. построить график исходного временного ряда и визуально оценить наличие в нем тенденции и возможный ее тип. Сгладить исходный временной ряд с помощью скользящей средней (шаг сглаживания равен 3). Построить график сглаженного ряда и визуально оценить возможный в нем тип тенденции. Оба графика построить на одном чертеже (рис. 2). Результаты обеих визуальных оценок отметить в отчете;
2. оценить с помощью метода Фостера – Стюарта и коэффициента Кендела наличие тенденции (в среднем и дисперсии) в исходном временном ряде. Сравнить полученные оценки с оценками, полученными при выполнении пункта 1, и сделать окончательный свой вывод. Результаты вывода отметить в отчете;
3. по исходным данным методом усреднения по левой и правой половине определить параметры линейного тренда ![]() = а0 + а1 t. Построить график исходного временного ряда и полученного линейного тренда на одном чертеже (рис. 3). Оценить визуально, отражает ли линейный тренд тенденцию временного ряда? Свой вывод отразить в отчете;
= а0 + а1 t. Построить график исходного временного ряда и полученного линейного тренда на одном чертеже (рис. 3). Оценить визуально, отражает ли линейный тренд тенденцию временного ряда? Свой вывод отразить в отчете;
4. по исходным данным методом МНК рассчитать параметры линейного тренда ![]() = а0 + а1 t. Кроме того, выбрать нелинейную модель, которая, по вашему мнению, может хорошо описать тенденцию исходного временного ряда. Рассчитать параметры выбранной вами нелинейной трендовой модели. Построить три графика (исходный временной ряд, линейная и выбранная вами нелинейная трендовая модели) на одном чертеже (рис. 4). Определить аналитическим способом, какая из двух трендовых моделей (линейная и нелинейная) наилучшим образом аппроксимирует исходный временной ряд;
= а0 + а1 t. Кроме того, выбрать нелинейную модель, которая, по вашему мнению, может хорошо описать тенденцию исходного временного ряда. Рассчитать параметры выбранной вами нелинейной трендовой модели. Построить три графика (исходный временной ряд, линейная и выбранная вами нелинейная трендовая модели) на одном чертеже (рис. 4). Определить аналитическим способом, какая из двух трендовых моделей (линейная и нелинейная) наилучшим образом аппроксимирует исходный временной ряд;
5. построить график ряда отклонений еt (рис. 5) и визуально оценить отсутствие в нем тенденции. Оценить адекватность выбранной модели тренда исходному ряду на основе анализа данных ряда отклонений;
6. рассчитать точечную и интервальную прогнозную оценку с периодом упреждения, равным t = 1.
1)
| t | yt | Скользящая сумма 3 уровней | Скользящая средняя из 3 уровней |
| 1 | 11,9 | - | |
| 2 | 12,6 | 36,7 | 18,35 |
| 3 | 12,2 | 38,7 | 19,35 |
| 4 | 13,9 | 40,4 | 20,2 |
| 5 | 14,3 | 42,8 | 21,4 |
| 6 | 14,6 | 44,2 | 22,1 |
| 7 | 15,3 | 44,3 | 22,15 |
| 8 | 14,4 | 45,5 | 22,75 |
| 9 | 15,8 | 46,9 | 23,45 |
| 10 | 16,7 | 49,9 | 24,95 |
| 11 | 17,4 | 50,2 | 25,1 |
| 12 | 16,1 | - | - |
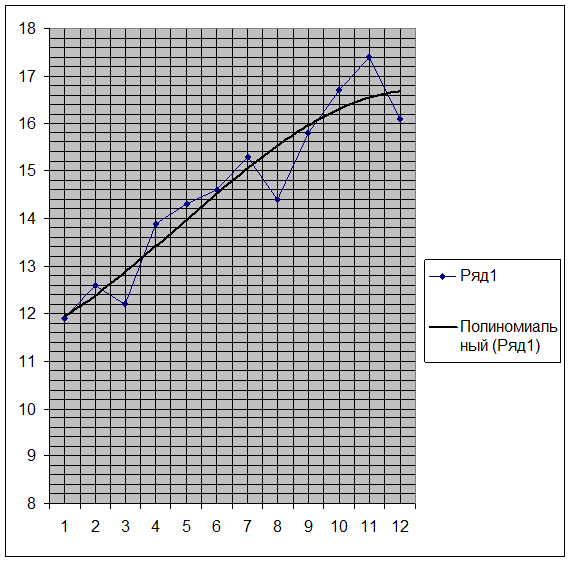
Рис. 2. Еженедельный оборот магазина «Ткани для дома» (исходный и сглаженный ряд)
После построения графика (рис. 2) можно сделать вывод о наличии возрастающей тенденции. После построения сглаженного ряда стало более наглядно видно наличие возрастающей тенденции.
2). а) Метод Фостера – Стюарта
| t | Yt | Ut | lt | S | D | Pt |
| 1 | 11,9 | - | - | - | - | - |
| 2 | 12,6 | 1 | 0 | 1 | 1 | 1 |
| 3 | 12,2 | 0 | 0 | 0 | 0 | 1 |
| 4 | 13,9 | 1 | 0 | 1 | 1 | 3 |
| 5 | 14,3 | 1 | 0 | 1 | 1 | 4 |
| 6 | 14,6 | 1 | 0 | 1 | 1 | 5 |
| 7 | 15,3 | 1 | 0 | 1 | 1 | 6 |
| 8 | 14,4 | 0 | 0 | 0 | 0 | 5 |
| 9 | 15,8 | 1 | 0 | 1 | 1 | 8 |
| 10 | 16,7 | 1 | 0 | 1 | 1 | 9 |
| 11 | 17,4 | 1 | 0 | 1 | 1 | 10 |
| 12 | 16,1 | 0 | 0 | 0 | 0 | 9 |
| 175,2 | 8 | 8 | 61 |
Выдвинем нулевую гипотезу: во временном ряде (данные графы 2) нет тенденции среднего уровня и нет тенденции дисперсии. Для проверки выдвинутой нулевой гипотезы необходимо рассчитать по формулам 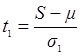 и
и 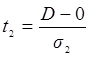 значения t1 и t2 . Но для этого надо знать значения μ, σ1 ,σ2 . В приложении 1 приведены данные для n=10 и для n=15, а нам надо найти данные для n=12.
значения t1 и t2 . Но для этого надо знать значения μ, σ1 ,σ2 . В приложении 1 приведены данные для n=10 и для n=15, а нам надо найти данные для n=12.
Для нахождения данных при n=12 используем принцип интерполяции, предположив, что эти данные в интервале от n=10 до n=15 изменяются линейно, т.е. равномерно. Поэтому нам нужно к значениям данных при n=10 прибавить их изменения за два (2=12–10) шага и получить искомые данных.
Найдем μ для n=12 следующим образом. Значение μ для n=10, согласно приложению 1, равно 3,858. Увеличение μ при изменении n на 2 шага найдем следующим образом
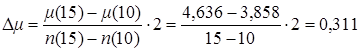 .
.
Отсюда μ(12)=μ(10)+Δμ=3,858+0,311=4,169. Аналогичным образом найдем значения для σ1 (12)=1,381 и для σ2 (12)=2,040. По формулам (2.7) найдем значения t1 и t2
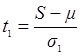 = (8 – 4,169)/1,381 = 3,326;
= (8 – 4,169)/1,381 = 3,326; 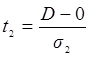 = (8-0)/2,040 = 3,92
= (8-0)/2,040 = 3,92
Случайные величины t1 и t2 имеют распределение Стьюдента с числом степеней свободы К = n – 1 = 12 – 1 = 11 и уровнем значимости a, который может принимать значения 0,01; 0,05 и т.д. Примем уровень значимости (вероятность, с которой исследователь может ошибиться), равный 0,05 (5%). На основе выбранного уровня значимости а = 0,05 рассчитаем доверительную вероятность: g = 1 – а = 1 – 0,05 = 0,95.
По числу степеней свободы К = 11 и величине доверительной вероятности g = 0,95 по таблице «Значение t-критерия Стьюдента» (Приложение 1)определим табличное значение случайной величины (tg ): tg = 2,201.
Расчетные значения t1 и t2 сопоставим с табличным tg .
Если сопоставить расчетные значения t1 и t2 с табличным tg , то может возникнуть четыре ситуации.
1) |t1 | > |tg |.