Курсовая работа: Расчет линейных электрических цепей переменного тока
I CA = ![]() =
= 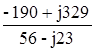 = -4,96+j3,83 = 6,27
= -4,96+j3,83 = 6,27![]() A
A
Систему линейных токов определяем из соотношений:
I A = I AB – I CA = j5,85+4,96-j3,83 = 4,96+j2,02 = 5,36![]() A
A
I B = I BC – I AB = -6,32+j1,81-j5,85 = -6,32-j4,04 = 7,5![]() A
A
I C = I CA – I BC = -4,96+j3,83+6,32-j1,81 = 1,36+j1,92 =2,35![]() A
A
Определяем мощности фаз приемника:
S AB =IAB 2 *Z 1 = 5,852 *(-j65) = -j2224 = 2224![]() B*A.
B*A.
S BC = IBC 2 *Z 2 = 6,582 *(14+j56) = 606+j2425 = 2499![]() B*A.
B*A.
S CA = ICA 2 *Z 3 = 6,272 *(56 – j23) =2201– j904 = 2380*![]() B*A.
B*A.
Определяем мощность трехфазной нагрузки:
S AB +S BC +S CA = -j2224+606+j2425+2201– j904 =2807 – j703 =
= 2894![]() B*A.
B*A. ![]()
Для построения векторной диаграммы задаёмся масштабами токов MI =1 A/см и напряжений MU = 50A/см. Векторная диаграмма построена на рисунке 10.
6 Расчёт неразветвлённой цепи с несинусоидальными напряжениями и токами
Составляем схему заданной цепи, подключая последовательно соединённые приёмники к источнику несинусоидального напряжения, под действием которого в цепи возникает ток с мгновенным значением
i=7Sin(wt+130 )+1,2Sin(2wt-860 )+0,4Sin3wt A,который на схеме замещения представляем как последовательно соединённые три источника переменного напряжения u1 , u2 и u3 c разными частотами (рисунок 11)
Величины сопротивлений заданы для частоты первой гармоники:
XC 11 = 18 Ом, R2 = 23 Ом, XL 21 = 14 Ом, R3 = 12 Ом, XC 31 = 62 Ом. Поскольку напряжения источников имеют разные частоты, то и реактивные сопротивления для них будут иметь разные величины. Активные сопротивления считаем от частоты не зависящими. Поэтому расчёт ведём методом наложения, то есть отдельно для каждой гармоники.
. 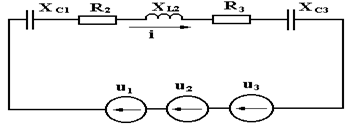
Рисунок 11.
Первая гармоника
Определяем активное и реактивное сопротивления всей цепи:
R = R2 + R3 = 14+56 = 70 Ом. X1 = -XC11 + XL21 - XC31 = - 65+56–23 =
= -32 Ом.
Полное сопротивление цепи:
Z1 = ![]() =
= ![]() = 76,7 Ом.
= 76,7 Ом.
Амплитудные значения напряжения и тока:
Im 1 = 7 A, Um 1 = Im 1 *Z1 = 7*76.7 =537 B.
Действующие значения напряжения и тока:
U1 = Um 1 / ![]() = 537 / 1,41 = 381 B.
= 537 / 1,41 = 381 B.