Курсовая работа: Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами

2 этап

Вид решения для i_3св при действии в цепи источников постоянного и переменного напряжений одинаков, так как в однородном дифференциальном уравнении отсутствует параметр U, а значит, вид i_3св не зависит от входного напряжения.

Таким образом, выражение, которое было найдено в 1этапе, будет иметь следующий вид:

i_3св =А₁ е^-406t +А₂ е^-234t

Теперь найдём вынужденную составляющую тока катушки i_3вын

i_3вын находим для цепи в послекоммутационном режиме. Расчёт параметров схемы при действии e(t);

Найдём вынужденную составляющую амплитудного тока I₁ , а для этого найдём Z_{п вын} сопротивление цепи:

Z_{п вын} = (Ом)

I_1m = (A)

Найдём U_{ab вын}

U_{ab m} = I_1m (В)

I_{3 m} =(A)

Найдём i_{3 вын}

I_{3 вын} = I_{3 m} sin(wt+j)=2.607sin(314t-43.60) (A)

Таким образом

i₃ =2.607sin(314t-43.60)+А₁ е^-406t +А₂ е^-234t

3^/ этап

Найдём А₁ и А₂ исходя из начальных условий, законов коммутации и на основании системы уравнений Кигхгофа записаных на 1^/ этапе.

i₃ =2.607sin(314t-43.60)+А₁ е^-406t +А₂ е^-234t

i₃₍₊₀₎ =i_3(-0) =-1.314 (A)

i₃₍₊₀₎ =2.607sin(-43.60)+A₁ +A₂ =-1.798+A₁ +A₂

R₁ i₁ =U(t)-R₂ i₂ -U_C

=

=

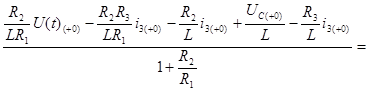
Подставим значение , i₃₍₊₀₎ , и найдём коэффициенты А₁ и А₂ для времени t+0