Курсовая работа: Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами

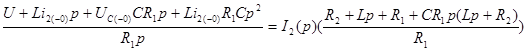
Подставим численные значения элементов

По полученному изображению найдём оригинал тока .

Операторное решение тока имеет вид правильной дроби I=. Оригинал тока найдём при помощи теоремы разложения.

Определим корни знамена теля, для этого приняв его равным нулю.

p₁ =0

0,000065p² +0,1065p+36=0

Д=(0б1065)² -4^. 0,000065^. 36=0,0019

I₂ (p)=

Найдём A₁ A₂ A₃

Коэффициент A_n будем искать в виде, где N(p) – числитель, а M(p) – знаменатель

A₁ =

A₂ =

A₃ =

Таким образом, i₂ (t) будет равняться

i₂ (t)=A₁ ^. exp(p₁ t)+ A₂ ^. exp(p₂ t)+ A₃ ^. exp(p₃ t)=1,944-0,71e^-477t +0,3e^-1162t

Искомый ток катушки i₂ равняется :

i₂ =1,944-0,71e^-477t +0,3e^-1162t (A)

Токи сходятся.

4 этап курсовой работы

Начертим схему для расчёта цепи интегралом Дюамеля и рассчитаем её

R3 R3

R1

i1

	C

ic

Определим переходную характеристику h¹ (t) цепи по напряжению U_R2 . Для этого рассчитаем схему при подключении цепи в начальный момент t=0 к источнику единичного напряжения. Рассчитаем схему классическим методом. Так как нулевые начальные условия U_C(-0) =U_C(+0) =0, это значит дополнительных ЕДС не будет.