Курсовая работа: Расчет плоских и пространственных конструкций
6. Провести анализ и исследование полученного решения:
o исследовать влияние вида опор и места их расположения на величины реакций внешних и внутренних связей.
o выбрать такое расположение опор, при котором обеспечивается минимальное количество сжатых или растянутых стержней (по указанию преподавателя);
o определить область допустимых значений ориентации опорной плоскости катковой опоры,
В процессе выполнения курсовой работы необходимо выработать следующие навыки и умения:
o определения связей, действующих на тело или систему тел;
o составления уравнений равновесия для произвольного тела, входящего в систему тел и нахождения реакций связей;
o решения поставленной задачи разными методами.
Мостовая ферма находится в равновесии под действием сил  ,
,  и
и  . Геометрические размеры фермы известны. Ферма опирается в точке
. Геометрические размеры фермы известны. Ферма опирается в точке  на катковую опору, а в точке
на катковую опору, а в точке  закреплена неподвижным шарниром.
закреплена неподвижным шарниром.
Исследовать равновесие фермы. Определить реакции внешних и внутренних связей для разных видов опор и мест их расположения (схемы 1, 2, 3).

Исходные данные
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Определение реакций внешних связей
Для определения реакций внешних связей рассмотрим мостовую ферму ![]() (рис. 2) содержащую 8 узлов, соединенных 13 стержнями. Ферма находится в равновесии под действием активных сил
(рис. 2) содержащую 8 узлов, соединенных 13 стержнями. Ферма находится в равновесии под действием активных сил ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и связей приложенных в точках
и связей приложенных в точках ![]() и
и ![]() .
.
Освободим ферму от опор, заменив их действие силами реакций связей ![]() . Проведем систему координат
. Проведем систему координат ![]() и изобразим действующие на нее внешние силы: активные
и изобразим действующие на нее внешние силы: активные ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и реакции связей
и реакции связей

Реакцию ![]() катковой опоры направим перпендикулярно опорной плоскости, а реакцию неподвижной шарнирной опоры
катковой опоры направим перпендикулярно опорной плоскости, а реакцию неподвижной шарнирной опоры ![]() –
– ![]() изобразим двумя составляющими
изобразим двумя составляющими ![]() и
и ![]() , т. е.
, т. е. ![]() , направив их в положительном направлении координатных осей. Так как все указанные силы расположены в плоскости
, направив их в положительном направлении координатных осей. Так как все указанные силы расположены в плоскости ![]() , то ферма находится в равновесии под действием произвольной плоской системы сил.
, то ферма находится в равновесии под действием произвольной плоской системы сил.
Так как на ферму действует произвольная плоская система сил и выполняется условие ![]() , то ферма является статически определимой и расчет фермы можно осуществить методами теоретической механики.
, то ферма является статически определимой и расчет фермы можно осуществить методами теоретической механики.
Составим уравнения равновесия системы сил, действующих на ферму:
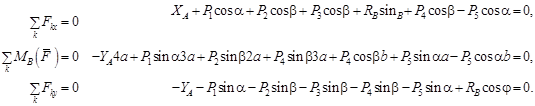
Последовательно решая систему уравнений , из второго уравнения найдем реакцию ![]()
![]()
Из третьего уравнения этой системы – ![]()
![]() ,
,
а из первого уравнения