Курсовая работа: Расчет плоских и пространственных конструкций
В некоторых случаях, если это обосновано критериями выбора, катковую опору можно заменить двухсторонней (удерживающей) связью, например стержнем. Угол 
, определяющий его положение, может изменяться в интервале 
.
Значения аргумента функций 
в этом случае могут быть найдены с точностью 
, величина которой определяется заданием шага ранжированной переменной , при построении графиков функций [1]. В нашем случае 
.
Для рассматриваемой фермы анализ результатов расчетов, проведенных в п. 4, дает следующее.
Схема 1
1. Реакция опорной плоскости 
положительна при всех допустимых значениях ориентации опорной плоскости
2. Количество стержней, реакция которых не зависит от 
– 10 (1,2, 3,4, 5, 6, 7,8, 9, 10) из них сжатых – 6 (2,5,6, 7,8,11 )
3. Максимальное значение сжимающего усилия, величина которого не зависит от угла , равно 
.
Схема 2
1. Реакция опорной плоскости 
положительна при всех допустимых значениях ориентации опорной плоскости
2. Количество стержней, реакция которых не зависит от – 10 (3,4, 5, 6, 7, 9, 10, 11, 12, 13), из них сжатых – 5 (2, 6, 7, 10, 13)
3. Максимальное значение сжимающего усилия, величина которого не зависит от угла , равно 
(рис. 11).
Схема 3
1. Реакция опорной плоскости положительна при всех допустимых значениях ориентации опорной плоскости (рис. 13)
.
2. Реакция опорной плоскости 
положительна при значениях угла не превышающих величину 
(рис. 13)
.
3. Стержень 
при разных значениях испытывает сжимающие и растягивающие усилия. В тоже время, сжимающее усилие в стержне
не будет превышать предельного значения 
при значениях угла меньших величины 
(рис. 13)
.
4. Количество стержней, реакция которых не зависит от – 7, из них сжатых – 5
5. Максимальное значение сжимающего усилия, величина которого не зависит от угла , равно 
(рис. 14).
С 2. Равновесие составных конструкЦий
Задача 119
Конструкция состоит из стержня ВС и АС, которые шарнирно соединены в точке С
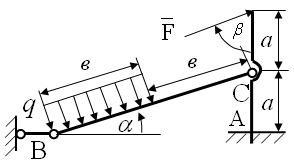
Внешними связями, наложенными на конструкцию, являются жёсткая заделка в точке А и невесомый стержень в точке В. Конструкция находится в равновесии под действием сосредоточенной силы 
и распределённой нагрузки, действующей на половине участка BC по линейному закону с интенсивностью 
.
Определить реакции внешних и внутренних Связей в точках А, B и С если
Для определения реакций связей расчленим конструкцию и рассмотрим равновесие каждой её части отдельно.
Рассмотрим равновесие стержня АС(рис 8).Проведём координатные оси xAy и изобразим действующие на стержень силы: силу 
и реакции связей. Реакцию жёсткой заделки А изобразим моментом МА и двумя составляющими 
и 
, реакцию шарнира С двумя её составляющими 
и 
.
Стержень АС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
|
|
|
К-во Просмотров: 689
Бесплатно скачать Курсовая работа: Расчет плоских и пространственных конструкций
|