Курсовая работа: Расчет плоских и пространственных конструкций

Для нахождения реакции составим уравнения моментов, относительно точки Риттера:

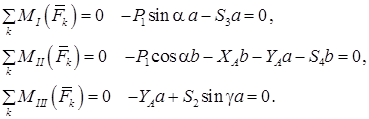(26),(27),(28)

Для определения реакций стержней 8, 10 и 9 проведем сечение , и рассмотрим равновесие правой части фермы. На правую часть фермы действуют известные силы, а также реакции отброшенной части.

Для нахождения реакций составим уравнения моментов относительно точек Риттера соответственно:

,

4. Результаты расчетов

Решения систем линейных алгебраических уравнений – , – или – можно легко реализовать в пакете Mathcad или других математически ориентированных пакетах. Для этого система уравнений приводится к матричной форме

,

где – вектор правых частей, полностью определенный действующими на ферму активными силами;

– вектор неизвестных реакций внешних и внутренних связей S, задающийся в соответствии с обозначениями, принятыми на рис. 3, рис. 4 или рис. 5;

– матрица коэффициентов, которая формируется на основе двух матриц: постоянной – независящей от расположения опор фермы и переменной – зависящей от их расположения.

Решение сформированной системы уравнений ищется в виде

5. Анализ результатов вычислений

Методы теоретической механики при расчете ферм обычно применяются на этапе предварительного проектирования. Именно на этом этапе может быть поставлена задача выбора оптимального решения согласно одному или нескольким критериям.

Например, требуется обеспечить:

o минимальную силу давления на одну или все опоры;

o минимальное количество стержней, испытывающих сжимающие усилия;

o минимальное количество стержней, в которых сжимающие усилия не превышают некоторого предельного значения .

Также возможна комбинация этих критериев.

При такой постановке задачи расчет следует производить при экстремальных значениях действующих на ферму активных сил. В качестве влияющих параметров можно выбрать ориентацию опорной плоскости, характеризуемую углом , и (или) характерный размер фермы (определяется преподавателем).

Рассмотрим задачу выбора схемы расположения внешних связей, действующих на ферму, при которых сжимающие усилия не превышают некоторого предельного значения , а количество сжатых стержней минимально. В качестве такого критерия примем максимальное значение, не зависящее от угла , сжимающего усилия в стержнях фермы.

При анализе следует учесть:

o свойства катковых опор. Катковая опора является неудерживающей связью и, следовательно, ее реакция может быть только положительной (если она направлена перпендикулярно опорной плоскости вверх).

o особенности мостовых ферм. Для них ориентация опорной плоскости катковой опоры может характеризоваться только положительными значениями углов .

Учет вышесказанного требует исключения таких состояний, при которых

o углы , характеризующие ориентацию опорных плоскостей, отрицательны;

o реакции катковых опор неположительны.

Иными словами, область допустимых значений указанных величин определяется неравенствами