Курсовая работа: Разработка математической модели теплообменника смешения
Такие объекты называются статическими, а приведенная выше зависимость, которая связывает значения выходного и параметров объекта в установившемся режиме, называется их статической характеристикой.
Простейшем примером статического объекта регулирования может служить напорной бак (рис. 1.1).
математический модель теплообменник смешение
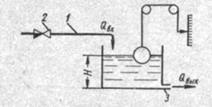
Рис 1.1.Напорный бак как объект регулирования уровня (где 1-входная труба,2-клапан,3-сливная труба)
Жидкость поступает в него по трубе 1 через клапан 2 и свободно вытекает по сливной трубе 3. Входным сигналом для этого объекта, очевидно, является изменение расхода Qвх жидкости через клапан 2, а выходным — изменение уровня Н.
Если приток и сток равны, то количество находящейся в баке жидкости остается постоянным и ее уровень не изменяется. Это статический режим работы объекта, который описывается уравнением материального баланса:
![]() (1.3)
(1.3)
где![]() — расход жидкости через сливную трубу 3.
— расход жидкости через сливную трубу 3.
Известно, что расход жидкости при свободном истечении зависит от уровня и с достаточной точностью описывается уравнением
![]() (1.4)
(1.4)
Где ![]() — коэффициент пропорциональности, который зависит от размеров и формы отверстия истечения. Подставим значение
— коэффициент пропорциональности, который зависит от размеров и формы отверстия истечения. Подставим значение ![]() в (1.3) и после выполнения необходимых преобразований получим уравнение статической характеристики бака в виде
в (1.3) и после выполнения необходимых преобразований получим уравнение статической характеристики бака в виде
![]() (1.5)
(1.5)
где![]() -коэффициент пропорциональности.
-коэффициент пропорциональности.
Это нелинейное уравнение и график статической характеристики такого объекта (рис. 1.2) также нелинеен. Если в состав САР входит хотя бы один нелинейный элемент, то такая САР также называется нелинейной. Анализ подобных систем чрезвычайно трудоемок, а во многих случаях он вообще невозможен. Поэтому всегда, когда это возможно, стремятся заменить нелинейную математическую модель линейной, которая, хотя и менее точна, но поддается анализу стандартными, хорошо разработанными и относительно простыми методами. Замена нелинейной математической модели более грубой линейной с целью упрощения анализа и синтеза САР называется линеаризацией модели[1].
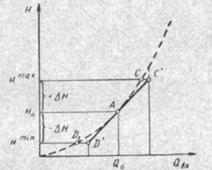
Рис 1.2.Статическая характеристика напорного бака.
Наиболее простым является метод графической линеаризации, который применяется в тех случаях, когда статическая характеристика имеет вид плавной кривой. Линеаризация заключается в замене линейного участка характеристики в пределах возможного изменения входного и выходного параметров объекта прямой, касательной к статической характеристике в точке заданного режима работы. Рассмотрим применение этого метода на примере линеаризации характеристики напорного бака (рис. 1.2).
Предположим, что в баке должно поддерживаться заданное значение уровня ![]() с точностью
с точностью ![]() . Следовательно, рабочим участком статической характеристики служит криволинейный отрезок CAD, в середине которого находится рабочая точка А. Заменим его отрезком CAD' прямой, касательной к статической характеристике в рабочей точке, который и будет линеаризованной статической характеристикой данного объекта регулирования. Погрешность такой аппроксимации будет тем больше, чем больше отрезки СС и DD', которые зависят от кривизны истинной статической характеристики в окрестностях точки А и допустимого диапазона изменения регулируемого параметра (т. е. величины рабочего участка характеристики). Следует отметить, что если в процессе работы САР регулируемый параметр по каким-либо причинам выйдет за пределы рабочего участка статической характеристики, принятые при линеаризации, то это может привести к существенному ухудшению качества регулирования.
. Следовательно, рабочим участком статической характеристики служит криволинейный отрезок CAD, в середине которого находится рабочая точка А. Заменим его отрезком CAD' прямой, касательной к статической характеристике в рабочей точке, который и будет линеаризованной статической характеристикой данного объекта регулирования. Погрешность такой аппроксимации будет тем больше, чем больше отрезки СС и DD', которые зависят от кривизны истинной статической характеристики в окрестностях точки А и допустимого диапазона изменения регулируемого параметра (т. е. величины рабочего участка характеристики). Следует отметить, что если в процессе работы САР регулируемый параметр по каким-либо причинам выйдет за пределы рабочего участка статической характеристики, принятые при линеаризации, то это может привести к существенному ухудшению качества регулирования.
Математической основой данного метода линеаризации является разложение функции, описывающей статическую характеристику, в ряд Тейлора по малым приращениям входного сигнала ![]() иограничением ряда линейным членом. Проиллюстрируем возможности этого метода на том же примере напорного бака. Разложение функции (1.5) в ряд Тейлора по малым приращениям параметра
иограничением ряда линейным членом. Проиллюстрируем возможности этого метода на том же примере напорного бака. Разложение функции (1.5) в ряд Тейлора по малым приращениям параметра ![]() в окрестностях рабочей точки (т. е. при
в окрестностях рабочей точки (т. е. при ![]() ) имеет вид
) имеет вид
![]() (1.6)
(1.6)
Пренебрегая членами ряда, в которые входит сомножитель ![]() во второй и более высокой степени, и обозначая
во второй и более высокой степени, и обозначая ![]() получим линеаризованное статической характеристики бака
получим линеаризованное статической характеристики бака
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
Графически это уравнение соответствует отрезку прямой CAD' па рис. 1.2.
Кроме статических, существуют объекты регулирования, у которых при работе в статическом режиме отсутствует однозначная зависимость между входным и выходным сигналами. Такие объекты называются астатическими.
Примером простейшего астатического объекта регулирования может служить бак, из которого жидкость откачивается насосом постоянной производительности (рис. 1.3). У такого объекта состояние равновесия возможно только в одном случае — когда приток жидкости в бак равен производительности насоса.

Рис 1.3.Астатический обьект регулирования(1-регулирующий клапан,2-бак,3-насос постоянной производительности)