по каналу

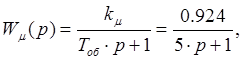(2.5)

3. Получение математической модели объекта в виде переменных пространство состояний

Одной из распространенных форм математического описания линейных динамических систем являются уравнения следующего вида:

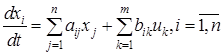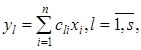; (3.1)

Это название связано с тем, что при u_k = 0 достаточно задать начальное значение переменных x_i , чтобы однозначно определить состояние системы x_i (t), y₁ для любого момента времени. Модель (3.1) содержит n дифференциальных уравнений 1-го порядка с k управляющими входными воздействиями, а также s алгебраических соотношений для связи выходных переменных системы y с переменными состояния x. Коэффициенты a_ij , b_ik , c_li называют параметрами модели.

Уравнения (3.1) удобно представить в матричной форме

(3.2)

где X - вектор переменных состояния; U − вектор управляющих (входных) воздействий; Y - вектор выходов; A, B, C − матрицы параметров [2].

Модель (3.2), в сравнении с ранее рассмотренными моделями, формирует дополнительно n переменных внутреннего состояния системы, что увеличивает количество информации об объекте управления.

При этом начальные условия согласуют следующим образом:

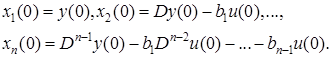(3.7)

Структурная схема объекта с учетом полученных передаточных функций:

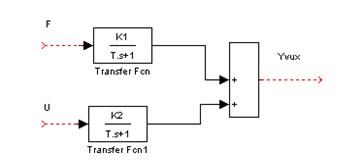
Рисунок 3.1-Структурная схема объекта

Тогда вектор переменных состояния объекта в отклонениях от желаемых базовых значений примет вид:

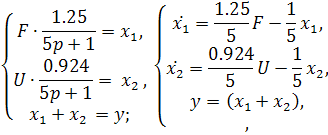
На основе полученных дифференциальных уравнений запишем матрицы А, B и S.

4. Получение дискретной математической модели объекта

Термин “дискретный” еще не сложился. Каждая система управления, в которой присутствует хотя бы один элемент, который не подчиняется непрерывному характеру изменения сигнала, может быть отнесен к классу дискретных систем. Для этих систем характерным является исчезновения сигнала информации хотя бы на небольшом интервале времени. Если эти интервалы устремить к нулю, то можно рассматривать систему как непрерывную. Дискретные системы более общие. В производстве часто технологические процессы непрерывные [2].

Пусть имеется на входе в дискретный элемент какой-то непрерывный сигнал. Введем период квантования. Заменяем реальное время на кванты т=к*Т к=0,1,…,. Если Т 0 тогда имеем непрерывную модель. В этом случае можно зафиксировать амплитуды. Кроме квантования по времени можно квантовать и по вертикали (амплитуде). При таком виде квантования цифры заносятся в виде “0” и “1”. В случае объединения этих квантований они называются дискретными.

Выделим случай, когда входной сигнал x(t) является элементарной функцией 1(t). Реакцию системы на воздействие 1(t) можно компактно:

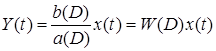, (5.1)

где W(D) называется операторной передаточной функцией или оператором. Формально W(D) можно рассматривать как дробно-рациональную функцию от оператора:

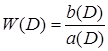. (5.2)

Воспользуемся преобразованием Лапласа, основываясь на утверждении

, (5.3)

если f(0) = 0. Аналогично можно записать:

(5.4)

(5.5)