(1.13)

где V₀ — рабочий объем смесителя (V₀ = const).

Подставим значение из (1.11) в (1.12) и после очевидных преобразований, переходя к пределу при , получим уравнение, описывающее динамическую характеристику данного объекта:

(1.14)

Выведенное ранее уравнение статической характеристики (1.13) может быть получено из (1.13) при выполнения условия равновесия, т.е когда Для приведения уравнения (1.14) к безразмерной форме введем следующее обозначение:

Подставляя данные из таблицы 1.1 получим следующее:

(1.15)

(1.16)

(1.17)

После подстановки их в уравнение (1.14) и проведения необходимых преобразований получим в оканчательном виде.

(1.18)

(1.19)

(1.20)

Преобразуем в область Лапласа

2. Получение передаточных функций по заданным динамическим каналам объекта

Передаточные функции характеризуют изменение сигнала при прохождении через систему.

Отношение Лапласовых изображений выходной и входной величин системы при нулевых начальных условиях называется передаточной функцией системы W(p)

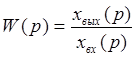(2.1)

где x_вх (p) и x_вых (p) – изображение по Лапласу входной и выходной величин системы.

По передаточной функции системы W(p) и изображению ее входной величины можно найти изображение выходной величины

(2.2)

При наличии одной входной и одной выходной величины система или звено имеют только один канал прохождения сигнала, а следовательно, и одну передаточную функцию. Если же система или звено имеют несколько каналов прохождения сигнала, что возможно при нескольких выходных и входных величинах, то прохождение сигнала в каждом канале характеризуется своей передаточной функцией[2].

Передаточные функции теплообменника могут быть найдены по его уравнению динамики, а также по структурной схеме (рис.2.1), составленной по равенствам (1.19).

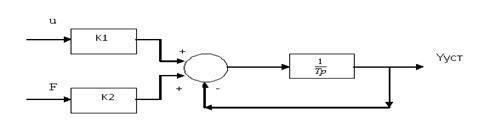
Рисунок 2.1-Структурная схема теплообменника смешения.

Приведем без вывода передаточные функции теплообменника:

(2.3)

по каналу