Курсовая работа: Разработка математической модели теплообменника смешения

В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его нормированная (приведенная к единице) переходная характеристика может быть аппроксимирована передаточной функцией вида:

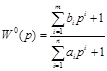(6.1)

Порядок числителя в выражении (6.1) всегда меньше или равен порядку знаменателя. Для нахождения явного вида выражения (6.1) для конкретного технологического объекта необходимо определить значения коэффициентов a_i и b_i , а также значения степеней полиномов n и m.

На первом этапе осуществляют нормирование переходной характеристики и входного воздействия:

;

(6.2)

Искомые коэффициенты W₀ (p) определяются из системы уравнений:

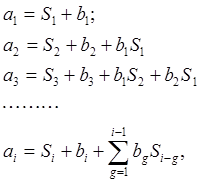(6.3)

где i=m+n и для всех i>n a_i =0, а для всех i>m b_i =0.

Входящие в эту систему уравнений коэффициенты S1, S2, …, Si связаны с кривой разгона интегральными соотношениями и вычисляются в соответствии с (4), где обозначено 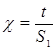- относительное время.Для расчета S1, S2 … Si используют численные методы (метод прямоугольников, метод трапеций и др.):[2]

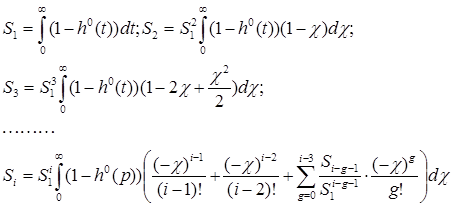(6.4)

Переход от нормированной передаточной функции к обычной осуществляется путем ее умножения на коэффициент передачи

: (6.5)

Программа расчет коэффициентов передаточной функции по экспериментальной переходной функции методом площадей в Matlab 6.5

clc,clear

T=0:1:30;

W=tf([1.25],[5 1])

y=step(W, T);

[T' y];

plot(T,y,'k');

grid

Таблица экспериментальных данных 6.1

t	y
0	0
1	0.22659
2	0.4121
3	0.56399
4	0.68834
5	0.79015
6	0.87351
7	0.94175
8	0.99763
9	1.0434
10	1.0808
11	1.1115
12	1.1366
13	1.1572
14	1.174
15	1.1878
16	1.199
17	1.2083
18	1.2158
19	1.222
20	1.2271
21	1.2313
22	1.2347
23	1.2374
24	1.2397
25	1.2416
26	1.2431
27	1.2444
28	1.2454
29	1.2462
30	1.2469

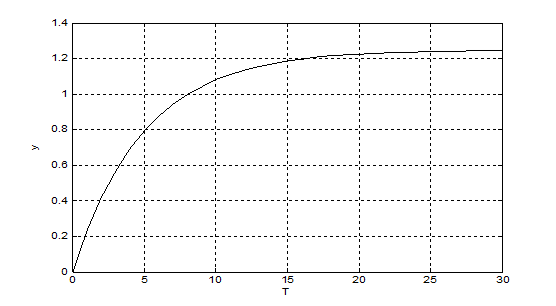
Рис.6-1. График переходной экспериментальной характеристики.

clear, clc

dt=1

h=[0 0.22659 0.4121 0.56399 0.68834 0.79015 0.87351 0.94175 0.99763 1.0434 1.0808 1.1115 1.1366 1.1572 1.174 1.1878 1.199 1.2083 1.2158 1.222 1.2271 1.2313 1.2347 1.2374 1.2397 1.2416 1.2431 1.2444 1.2454 1.2462 1.2469]

h1=h/1.25

n=length(h)