F=[0.25;0]

C=[1 1]

D=[0]

BB=[B F]

% переход в область переменных состояний

sistema1=ss(A,BB,C,D)

% переход в дискретную область

sistema2=c2d(sistema1,0.5)

Wz=tf(sistema2)

Модель в пространстве состояний.

a = x1 x2 x1 0.9048 0 x2 0 0.9048 b = u1 u2 x1 0 0.119 x2 0.08793 0

c = x1 x2 y1 1 1 d = u1 u2 y1 0

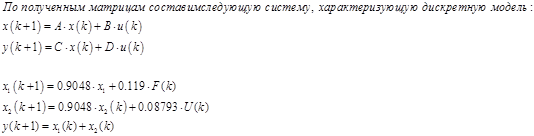
Передаточная функция в z-области по каналам.

1.По первому динамическому каналу.

5 . Получение переходных функций объекта по передаточным функциям каналов

Переходной характеристикой(переходной функцией) h(t) называется реакция системы на единичное ступенчатое входное воздействие u(t-τ)=1(t-τ) при нулевых начальных условиях. Единичная ступенчатая функция – это функция, которая обладает свойством

На рисунке 5.1 приведен пример переходной характеристики системы.

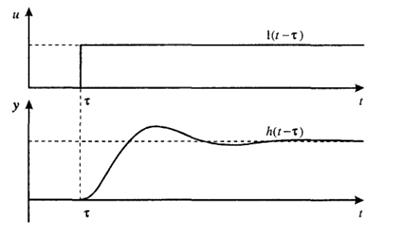
Рисунок 5.1-Пример переходной характеристики системы (τ – момент возникновения входного воздействия)

Для аналитического определения переходной функции следует решить дифференциальное уравнение при нулевых начальных условиях и единичном входном воздействии. При исследовании реального объекта переходную характеристику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Если входное воздействие представляет собой неединичную ступенчатую функцию u(t)=k1(t), то выходная величина будет равна y(t)=kh(t), т.е. представляет собой переходную характеристику с коэффициентом пропорциональности k[2].

Для построения переходной характеристики воспользуемся пакетом

Matlab:

clear,clc

W1=tf([1.25],[0.05 1]);

step(W)

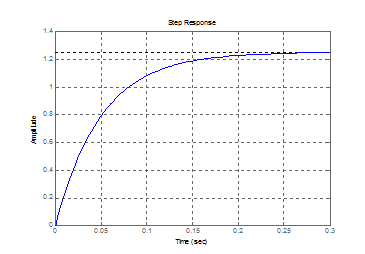
Рисунок 5.1- Переходная характеристика объекта по первому динамическому каналу