Курсовая работа: Разработка программы определительных испытаний
F25 = E25/$A$22, с последующим копированием в ячейки F26:F34
Колонку G заполним с помощью формулы:
G25 = E25, G26 = G25 + E26, с последующим копированием в ячейки G32:G39
Колонку H заполним с помощью формулы:
H25 = G25/$A$22, с последующим копированием в ячейки H26:H34
Данные, собранные в таблице 4 наглядно представим с помощью:
полигон частот – графическая зависимость частот (относительных частот) от середины интервалов (рисунок 1).
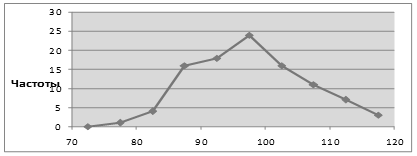
Рисунок 1 – Полигон частот
кумуляты частот – графическая зависимость накопленных частот (накопленных относительных частот) от середины интервалов (рисунок 2).
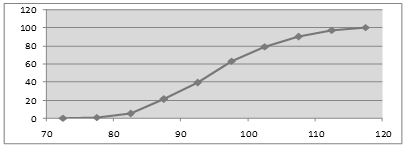
Рисунок 2 – Кумулята частот
1.6.4 Подбор подходящего закона распределения вероятностей
Далее рассмотрим некоторые известные распределения, такие как экспоненциальное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.
Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно гамма-распределение.
Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения. Таким образом, математическое ожидание случайной величины t равно выборочной средней, а среднее квадратическое отклонение случайной величины t – выборочному среднему квадратическому отклонению. Указанные характеристики находятся в ячейках F12 и F14 соответственно. Поместим эти значения в ячейки А2 и В2 соответственно (таблица 5).
Определим параметры экспоненциального (λ), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение) и гамма-распределения (α и β) в соответствии с формулами:
![]() ,
, ![]() ,
, ![]()
B5 = 1/A2;
B8 = A2;
B9 = B2;
B12 = (A2/B2)^2;
B13 = B2^2/A2.
Таблица 5 – Значения плотностей распределения
| A | B | C | D | E | |
| 1 | Матем. ожидание | Ср. кв. отклон. | |||
| 2 | 98,68 | 8,767340682 | |||
| 3 | |||||
| 4 | Параметры экспоненциального распределения | ||||
| 5 | λ | 0,0101 | |||
| 6 | |||||
| 7 | Параметры нормального распределения | ||||
| 8 | m | 98,6800 | |||
| 9 | σ | 8,767340682 | |||
| 10 | |||||
| 11 | Параметры гамма-распределения | ||||
| 12 | α | 126,6842 | |||
| 13 | β | 0,7789 | |||
| 14 | |||||
| 15 | Середина | Плотность относит. частот | Плотность экспоненц. распред. | Плотность нормал. распред. | Плотность гамма- распред. |
| 16 | 72,5000 | 0 | 0,0049 | 0,0005 | 0,0003 |
| 17 | 77,5000 | 0,002 | 0,0046 | 0,0025 | 0,0019 |
| 18 | 82,5000 | 0,008 | 0,0044 | 0,0083 | 0,0080 |
| 19 | 87,5000 | 0,032 | 0,0042 | 0,0202 | 0,0213 |
| 20 | 92,5000 | 0,036 | 0,0040 | 0,0355 | 0,0374 |
| 21 | 97,5000 | 0,048 | 0,0038 | 0,0451 | 0,0456 |
| 22 | 102,5000 | 0,032 | 0,0036 | 0,0414 | 0,0399 |
| 23 | 107,5000 | 0,022 | 0,0034 | 0,0274 | 0,0259 |
| 24 | 112,5000 | 0,014 | 0,0032 | 0,0131 | 0,0128 |
| 25 | 117,5000 | 0,006 | 0,0031 | 0,0045 | 0,0049 |
В ячейках В16:В25 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 4.
Плотности экспоненциального, нормального и гамма-распределений рассчитываются в соответствии с формулами:
С16 = ЭКСПРАСП (А16;$B$5;ЛОЖЬ);
D16 = НОРМРАСП (А16;$B$8;$B$9;ЛОЖЬ);
E16 = ГАММАРАСП (А16;$B$12;$B$13;ЛОЖЬ).
Затем копируем их в блок ячеек С17:Е25.