Курсовая работа: Разработка программы определительных испытаний

Рисунок 3 – Сглаживание гистограммы плотностью экспоненциального распределения

Рисунок 4 – Сглаживание гистограммы плотностью нормального распределения

Рисунок 5 – Сглаживание гистограммы плотностью гамма-распределения

Используя критерий χ² , установим, верна ли принятая гипотеза о том, что статистические данные подчиняются нормальному распределению.

Для применения критерия χ² необходимо, чтобы частоты n_i , соответствующие каждому интервалу, были не меньше 5. Для этого при необходимости объединим рядом стоящие интервалы, а их частоты суммируем. Далее вычислим следующую сумму:

,

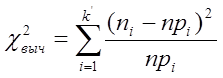где p_i – теоретическая вероятность того, что случайная величина Х примет значение из интервала [a_{i -1} ,a_i ].

Предположим, что случайная величина t имеет функцию распределения F(t), поэтому p_i = F(a_i ) – F(a_{i -1} ).

Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.

В колонке А содержатся левые, а в колонке В – праве границы интервалов. В колонке С находятся соответствующие частоты. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения.

Для экспоненциального распределения:

D31 = ЭКСПРАСП (B31; $B$5; ИСТИНА) – ЭКСПРАСП (А31; $B$5; ИСТИНА);

Для нормального распределения:

D40 = НОРМРАСП (В40; $B$8; $B$9; ИСТИНА) – НОРМРАСП (А40; $B$8; $B$9; ИСТИНА);

Для гамма-распределения:

D49 = ГАММАРАСП (В49; $B$12; $B$13; ИСТИНА) – ГАММАРАСП (А49; $B$12; $B$13$ ИСТИНА).

В колонке Е рассчитываются слагаемые соотношения по формуле:

Е31 = (С31-100*В31)^2/(100*D31), которая копируется в другие ячейки колонки Е.

После чего для каждого рассмотренного распределения определим итоговые суммы:

Е38 = СУММ(E34:E39);

Е47 = СУММ(E42:E47);

Е56 = СУММ(Е50:Е55).

Которые равны соответственно 659,6862; 5,2199 и 3,8740.

Гипотеза о виде закона распределения должна быть принята, если вычисленное значение χ² _выч достаточно мало, а именно не превосходит критического значения χ² _кр , которое определяется по распределению χ² в зависимости от заданного уровня значимости α и числа степеней свободы r=k^’ – s – 1. где k^’ – количество интервалов после объединения; s – число неизвестных параметров распределения, которые были определены по выборке.

В данном примере r = 7 – 2 – 1 = 2

Критическое значение рассчитывается по формуле: