Курсовая работа: Решение линейных интегральных уравнений

Чем лемма 1 доказана полностью.

Пусть, как и выше f(P) и K(P,Q),

(7)

и величина γ₀ определена равенством (3)

Покажем, что для приближённого решения уравнения (7) можно использовать квадратные формулы с неравномерными сетками.

Теорема 1. Пусть p- простое число, N=p, и величина n определена равенством

Тогда при произвольно малом ε для решения уравнения (7) выполняется асимптотическое равенство

где

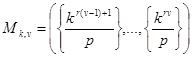
Доказательство.

Пусть функция Φ принадлежит классу и σ-сумма модулей её коэффициентов Фурье. Тогда согласно теореме 15 (1, с.94) справедлива квадратурная формула

, (8)

где

(9)

Выберем в лемме 1 . Тогда при для решения уравнения получим

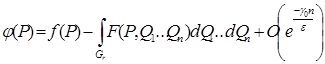(10)

где согласно (4)функция F(P,Q₁ ,…,Q_n ) определена равенством F(P,Q₁ ,…,Q_n )=и принадлежит классу.

Пусть при k=1,2,…,N и v=1,2,…,n точки M_{k , v} определены равенством

.

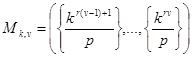Выберем p настолько большим, чтобы выполнялись неравенства n≥1 и N≥rn

Тогда применяя квадратичную формулу (8) получим

(11)

где в силу (9)

(12)

Пользуясь определением n и , получим

.