Курсовая работа: Решение линейных интегральных уравнений
Следовательно,
, 
, 
.
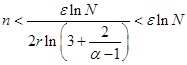В силу (12)
Но тогда из (10) и (11) следует, что
Отсюда, пользуясь оценкой
,
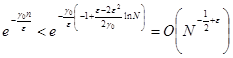получаем утверждение теоремы.
Результат, полученный в теореме 1, можно усилить, если воспользоваться методом оптимальных коэффициентов.
Лемма 2. Для всякого простого p существуют оптимальные коэффициенты a1 ,…,as такие, что каково бы ни было a>1+ε1 , при любом ε1 
(0;1) выполняется оценка
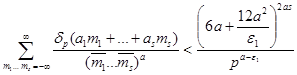
Доказательство.
Пусть z-произвольное целое из интервала Определим функцию Тs (z) равенством
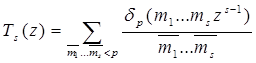
Пусть при z=a достигается минимум этой функции. Тогда, очевидно,
(13)
Так согласно лемме 1(1, с.21)
,
то при произвольном ε > 0 получим из (13),
Отсюда следует, что
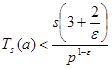(14)
Введём обозначения
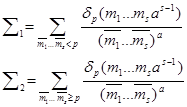
Так из (14) в силу определения величины Ts (a) следует оценка
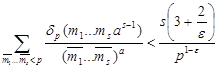(15)
то пользуясь неравенством, получим