Курсовая работа: Решение линейных интегральных уравнений

Чтобы оценить сумму Σ₂ , заметим, что для нетривиальных решений сравнения

(17)

Выполняется неравенство

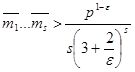(18)

Действительно, согласно определению величины δ_p (m) в левой части неравенства (14) отличны от нуля только такие слагаемые, для которых m₁ ,…,m_s является нетривиальным решением сравнения (5.43). так как любое из этих слагаемых не превосходит всей суммы, то для каждого нетривиального решения сравнения получим

,

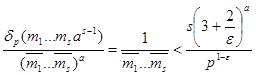Чем неравенство (5.44) доказано.

Пусть функция φ(m₁ ,…,m_s ) определена равенствами

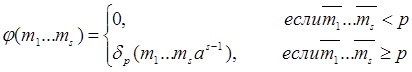
Тогда пользуясь леммой 18 (1, c.101), получим

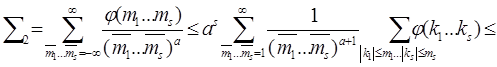
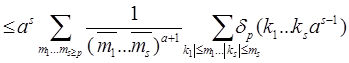. (19)

Обозначим через q минимальное значение произведения , где m₁ ,…,m_s –произвольное нетривиальное решение сравнения (17).

Тогда, выбирая в лемме 26 (1, с.151)

,

получим, что при любых натуральных m₁ ,…,m_{s ,} удовлетворяющих условию m₁ ,…,m_s p, выполняется оценка

.

Пользуясь этой оценкой и замечая, что в силу (18)

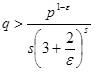
при любом ε ≤ a-1 положительном получим из (19)

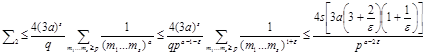(20)

Выберем a_v =a^v-1 (v=1,2,…,s) (21)

тогда, пользуясь оценками (16) и (20), при получим неравенство, указанное в лемме:

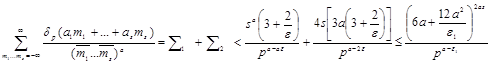
Для завершения доказательства леммы остается убедиться, что величины , определенные равенством (21), являются оптимальными коэффициентами.

Действительно, из (5.39), пользуясь леммой 1(1, c.21) получим

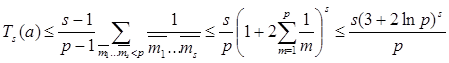
Переписывая эту оценку в виде