Курсовая работа: Решение параболических уравнений
Сетка может состоять из клеток разной конфигурации: квадратных, прямоугольных, треугольных и других. После построения сетки исходное дифференциальное уравнение заменяется разностным уравнением во всех внутренних узлах сетки. Затем на основании граничных условий устанавливаются значения искомого решения в граничных узлах. Присоединяя граничные условия сеточной задачи к разностным уравнениям, записанных для внутренних узлов, получаем систему уравнений, из которой определяем значения искомого решения во всех узлах сетки.
Замена дифференциального уравнения разностным может быть осуществлена разными способами. Один из способов аппроксимации состоит в том, что производные, входящие в дифференциальное уравнение, заменяются линейными комбинациями значений функции ![]() в узлах сетки по тем или иным формулам численного дифференцирования. Различные формулы численного дифференцирования имеют разную точность, поэтому от выбора формул аппроксимации зависит качество аппроксимации дифференциального уравнения разностным уравнением.
в узлах сетки по тем или иным формулам численного дифференцирования. Различные формулы численного дифференцирования имеют разную точность, поэтому от выбора формул аппроксимации зависит качество аппроксимации дифференциального уравнения разностным уравнением.
Рассмотрим неоднородное уравнение теплопроводности, являющееся частным случаем уравнений параболического типа:
![]() , (1.2)
, (1.2)
![]() – известная функция.
– известная функция.
Будем искать решение этого уравнения в области
![]()
Заметим, что эту полуполосу всегда можно привести к полуполосе, когда ![]() . Уравнение (1.2) будем решать с начальными условиями:
. Уравнение (1.2) будем решать с начальными условиями:
![]() , (1.3)
, (1.3)
![]() – известная функция, и краевыми условиями:
– известная функция, и краевыми условиями:
 (1.4)
(1.4)
где ![]() – известные функции переменной
– известные функции переменной ![]() .
.
Для решения задачи область ![]() покроем сеткой
покроем сеткой ![]() .
.

Узлы сетки, лежащие на прямых ![]() ,
, ![]() и
и ![]() будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной
будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной  воспользуемся следующей формулой:
воспользуемся следующей формулой:
 .
.
Для производной ![]() запишем следующие формулы:
запишем следующие формулы:
 ,
,
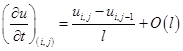 ,
,
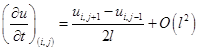 .
.
Можем получить три вида разностных уравнений:
![]() , (1.5)
, (1.5)
![]() , (1.6)
, (1.6)
![]() , (1.7)
, (1.7)
![]() .
.
Разностные уравнения (1.5) аппроксимируют уравнение (1.2) с погрешностью ![]() , уравнение (1.6) – с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью
, уравнение (1.6) – с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью ![]() .
.
В разностной схеме (1.5) задействованы 4 узла. Конфигурация схемы (1.5) имеет вид:
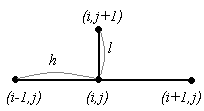
В схеме (1.6) также участвуют 4 узла, и эта схема имеет вид: