Курсовая работа: Решение параболических уравнений

– шаг по оси .

Заменив в каждом узле производные конечно-разностными отношениями по неявной схеме, получим систему вида:

. (1.31)

Преобразовав ее, получим:

, (1.32)

где

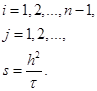
В граничных узлах

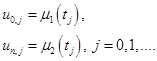(1.33)

В начальный момент

. (1.34)

Эта разностная схема устойчива при любом . Будем решать систему уравнений (1.32), (1.33) и (1.34) методом прогонки. Для этого ищем значения функции в узле в виде

, (1.35)

где – пока неизвестные коэффициенты.

Аналогично

. (1.36)

Подставив значение (1.35) в (1.32) получим:

.

Откуда

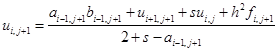. (1.37)

Из сравнения (1.35) и (1.37) видно, что

. (1.38)

. (1.39)

Для из (1.32) имеем:

.

Откуда

или

.