Курсовая работа: Решение параболических уравнений

В схеме (1.7) участвуют 5 узлов, и эта схема имеет вид:

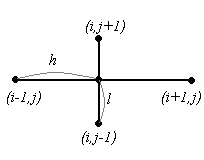
Первая и третья схемы – явные, вторая схема неявная. В случае явных схем значения функции в узле очередного слоя можно найти, зная значения в узлах предыдущих слоев. В случае неявных схем для нахождения значений решения в узлах очередного слоя приходится решать систему уравнений.

Для узлов начального (нулевого) слоя значения решения выписываются с помощью начального условия (1.3):

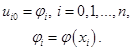(1.8)

Для граничных узлов, лежащих на прямых и , заменив производные по формулам численного дифференцирования, получаем из граничных условий (1.4) следующие уравнения:

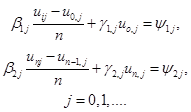(1.9)

Уравнения (1.9) аппроксимируют граничные условия (1.4) с погрешностью , так как используем односторонние формулы численного дифференцирования. Погрешность аппроксимации можно понизить, если использовать более точные односторонние (с тремя узлами) формулы численного дифференцирования.

Присоединяя к системе разностных уравнений, записанных для внутренних узлов, начальные и граничные условия (1.8) и (1.9) для разностной задачи получим полные разностные схемы трех видов. Для проведения вычислений самой простой схемой оказывается первая: достаточно на основании начального условия найти значения функции в узлах слоя , чтобы в дальнейшем последовательно определять значения решения в узлах слоев и т.д.

Третья схема также весьма проста для проведения вычислений, но при ее использовании необходимо кроме значений решения в узлах слоя найти каким-то образом значения функции и в слое . Далее вычислительный процесс легко организовывается. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи.

С точки зрения точечной аппроксимации третья схема самая точная.

Введем в рассмотрение параметр . Тогда наши разностные схемы можно переписать, вводя указанный параметр. При этом самый простой их вид будет при .

В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.

Разрешимость этой системы для явных схем вопросов не вызывает, так как все действия выполняются в явно определенной последовательности. В случае неявных схем разрешимость системы следует исследовать в каждом конкретном случае. Важным вопросом является вопрос о том, на сколько найденные решения хорошо (адекватно) отражают точные решения, и можно ли неограниченно сгущая сетку (уменьшая шаг по осям) получить приближенные решения, сколь угодно близкие к точным решениям? Это вопрос о сходимости метода сеток.

На практике следует применять сходящиеся разностные схемы, причем только те из них, которые являются устойчивыми, то есть при использовании которых небольшие ошибки в начальных или промежуточных результатах не приводят к большим отклонениям от точного решения. Всегда следует использовать устойчивые разностные схемы, проводя соответствующие исследования на устойчивость.

Первая из построенных выше разностных схем в случае первой краевой задачи будет устойчивой при . Вторая схема устойчива при всех значениях величины . Третья схема неустойчива для любых , что сводит на нет все ее преимущества и делает невозможной к применению на ЭВМ.

Явные схемы просты для организации вычислительного процесса, но имеют один весьма весомый недостаток: для их устойчивости приходится накладывать сильные ограничения на сетку. Неявные схемы свободны от этого недостатка, но есть другая трудность – надо решать системы уравнений большой размерности, что на практике при нахождении решения сложных уравнений в протяженной области с высокой степенью точности может потребовать больших объемов памяти ЭВМ и времени на ожидание конечного результата. К счастью, прогресс не стоит на месте и уже сейчас мощности современных ЭВМ вполне достаточно для решения поставленных перед ними задач.

1.2 Метод прогонки решения разностной задачи для уравнений параболического типа

Рассмотрим частный случай задачи, поставленной в предыдущем разделе. В области

найти решение уравнения

(1.10)

с граничными условиями

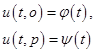(1.11)

и начальным условием

. (1.12)

Рассмотрим устойчивую вычислительную схему, для которой величина не является ограниченной сверху, а, значит, шаг по оси и может быть выбран достаточно крупным. Покроем область сеткой

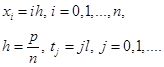
Запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (1.10) во всех внутренних узлах слоя . При этом будем использовать следующие формулы: