Курсовая работа: Решение систем дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка
2,200 4,4000 4,4000 0,0000 9,0250 9,0250 0,0000
2,400 4,8000 4,8000 0,0000 11,0232 11,0232 0,0000
2,600 5,2000 5,2000 0,0000 13,4637 13,4637 0,0000
2,800 5,6000 5,6000 0,0000 16,4446 16,4446 0,0000
3,000 6,0000 6,0000 0,0000 20,0855 20,0855 0,0000
3,200 6,4000 6,4000 0,0000 24,5325 24,5325 0,0000
3,400 6,8000 6,8000 0,0000 29,9641 29,9641 0,0000
3,600 7,2000 7,2000 0,0000 36,5982 36,5982 0,0000
3,800 7,6000 7,6000 0,0000 44,7012 44,7012 0,0000
4,000 8,0000 8,0000 0,0000 54,5981 54,5982 0,0000
Время выполнения: 0,015с
Как видно из полученного результата, точность в 0.0001 достигается уже при количестве шагов, равном 320. Время. Затраченное на расчёт таблицы значений на заданном интервале составляет всего 0.015 секунд, что практически не ощутимо. Увеличение шага сетки приведёт к повышению точности решения, однако это увеличит и время работы вычислительного процесса.
Заданная точность достигается за минимальное количество итерраций (1-3 итерации).
Ниже приведен график функций полученного и точного решений:
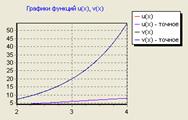
Рис. 5.1 График полученного и точного решения
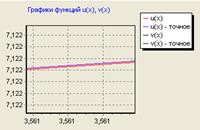
Рис. 5.2 График полученного и точного решения
Как видно из рисунков 5.1, 5.2, расхождение кривых наблюдается только при достаточно большом увеличении графика.
Предложенная задача Коши была также решена в математическом пакете “ Mathcad 11” двумя методами: методом Рунге-Кутта 5-го порядка и методом Рунге-Кутта с непостоянным шагом. Реализация решения системы дифференциальных уравнений в “ Mathcad 11” и таблицы результатов приведены ниже:
Реализация решения задачи Коши методом Рунге-Кутта 5-го порядка:
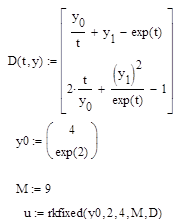
Таблица 5.1 – Результаты решения задачи Коши методом Рунге-Кутта 5-го порядка.
| x | u(x) | v(x) | x | u(x) | v(x) |
| 2 | 4 | 7,3890561 | 3,1 | 6,2 | 22,19795 |
| 2,02 | 4,04 | 7,5383249 | 3,12 | 6,24 | 22,64638 |
| 2,04 | 4,08 | 7,6906092 | 3,14 | 6,28 | 23,10387 |
| 2,06 | 4,12 | 7,8459698 | 3,16 | 6,32 | 23,5706 |
| 2,08 | 4,16 | 8,0044689 | 3,18 | 6,36 | 24,04675 |
| 2,1 | 4,2 | 8,1661699 | 3,2 | 6,4 | 24,53253 |
| 2,12 | 4,24 | 8,3311375 | 3,22 | 6,44 | 25,02812 |
| 2,14 | 4,28 | 8,4994376 | 3,24 | 6,48 | 25,53372 |
| 2,16 | 4,32 | 8,6711376 | 3,26 | 6,52 | 26,04954 |
| 2,18 | 4,36 | 8,8463062 | 3,28 | 6,56 | 26,57577 |
| 2,2 | 4,4 | 9,0250135 | 3,3 | 6,6 | 27,11264 |
| 2,22 | 4,44 | 9,2073308 | 3,32 | 6,64 | 27,66035 |
| 2,24 | 4,48 | 9,3933313 | 3,34 | 6,68 | 28,21913 |
| 2,26 | 4,52 | 9,5830891 | 3,36 | 6,72 | 28,78919 |
| 2,28 | 4,56 | 9,7766804 | 3,38 | 6,76 | 29,37077 |
| 2,3 | 4,6 | 9,9741824 | 3,4 | 6,8 | 29,9641 |
| 2,32 | 4,64 | 10,175674 | 3,42 | 6,84 | 30,56941 |
| 2,34 | 4,68 | 10,381237 | 3,44 | 6,879999 | 31,18696 |
| 2,36 | 4,72 | 10,590951 | 3,46 | 6,919999 | 31,81698 |
| 2,38 | 4,76 | 10,804903 | 3,48 | 6,959999 | 32,45972 |
| 2,4 | 4,8 | 11,023176 | 3,5 | 6,999999 | 33,11545 |
| 2,42 | 4,84 | 11,245859 | 3,52 | 7,039999 | 33,78443 |
| 2,44 | 4,88 | 11,473041 | 3,54 | 7,079999 | 34,46692 |
| 2,46 | 4,92 | 11,704811 | 3,56 | 7,119999 | 35,1632 |
| 2,48 | 4,96 | 11,941264 | 3,58 | 7,159999 | 35,87354 |
| 2,5 | 4,9999999 | 12,182494 | 3,6 | 7,199999 | 36,59823 |
| 2,52 | 5,0399999 | 12,428597 | 3,62 | 7,239999 | 37,33757 |
| 2,54 | 5,0799999 | 12,679671 | 3,64 | 7,279999 | 38,09184 |
| 2,56 | 5,1199999 | 12,935817 | 3,66 | 7,319999 | 38,86134 |
| 2,58 | 5,1599999 | 13,197138 | 3,68 | 7,359999 | 39,64639 |
| 2,6 | 5,1999999 | 13,463738 | 3,7 | 7,399999 | 40,4473 |
| 2,62 | 5,2399999 | 13,735723 | 3,72 | 7,439999 | 41,26439 |
| 2,64 | 5,2799999 | 14,013204 | 3,74 | 7,479999 | 42,09799 |
| 2,66 | 5,3199999 | 14,296289 | 3,76 | 7,519999 | 42,94842 |
| 2,68 | 5,3599999 | 14,585093 | 3,78 | 7,559999 | 43,81604 |
| 2,7 | 5,3999999 | 14,879732 | 3,8 | 7,599999 | 44,70118 |
| 2,72 | 5,4399999 | 15,180322 | 3,82 | 7,639999 | 45,60421 |
| 2,74 | 5,4799999 | 15,486985 | 3,84 | 7,679999 | 46,52547 |
| 2,76 | 5,5199999 | 15,799843 | 3,86 | 7,719999 | 47,46535 |
| 2,78 | 5,5599999 | 16,119021 | 3,88 | 7,759999 | 48,42421 |
| 2,8 | 5,5999999 | 16,444647 | 3,9 | 7,799999 | 49,40245 |
| 2,82 | 5,6399999 | 16,776851 | 3,92 | 7,839999 | 50,40044 |
| 2,84 | 5,6799999 | 17,115765 | 3,94 | 7,879999 | 51,4186 |
| 2,86 | 5,7199999 | 17,461527 | 3,96 | 7,919999 | 52,45732 |
| 2,88 | 5,7599999 | 17,814273 | 3,98 | 7,959998 | 53,51703 |
| 2,9 | 5,7999998 | 18,174145 | 4 | 7,999998 | 54,59815 |
| 2,92 | 5,8399998 | 18,541287 | |||
| 2,94 | 5,8799998 | 18,915846 | |||
| 2,96 | 5,9199998 | 19,297972 | |||
| 2,98 | 5,9599998 | 19,687816 | |||
| 3 | 5,9999998 | 20,085537 | |||
| 3,02 | 6,0399998 | 20,491291 | |||
| 3,04 | 6,0799998 | 20,905243 | |||
| 3,06 | 6,1199998 | 21,327557 | |||
| 3,08 | 6,1599998 | 21,758402 |
Реализация решения задачи Коши методом Рунге-Кутта с непостоянным шагом:
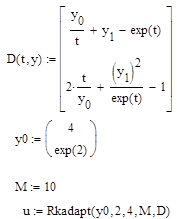
Таблица 5.2 – Результаты решения задачи Коши методом Рунге-Кутта с непостоянным шагом.
| X | u(x) | v(x) |
| 2 | 4 | 7,389056099 |
| 2,2 | 4,4 | 9,025013486 |
| 2,4 | 4,8 | 11,02317634 |
| 2,6 | 5,2 | 13,46373796 |
| 2,8 | 5,6 | 16,44464663 |
| 3 | 6 | 20,08553669 |
| 3,2 | 6,4 | 24,53252981 |
| 3,4 | 6,8 | 29,96409944 |
| 3,6 | 7,2 | 36,59823348 |
| 3,8 | 7,6 | 44,701183 |
| 4 | 8 | 54,59814775 |
Как видно из полученных таблиц результатов, точность решения в 0.0001 при решении методом Рунге-Кутта с непостоянным шагом достигается всего за 10 шагов, в то время, когда для достижения этой же точности при решении методом Рунге-Кутта 5-го порядка с постоянным шагом требуется около 100 шагов.
Сравнивая полученные результаты с результатами работы программы “Adams3.exe”, приходим к выводу, что неявная схема Адамса третьего порядка достаточно эффективна при численном решении задачи Коши (быстрота, высокая точность решения), однако по своим характеристикам она уступает более совершенным методам, применяющимися в различных математических пакетах.
Заключение
Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности.