Курсовая работа: Рішення задач цілочисленного програмування

Використовуючи для цього вираження формулу (17), одержимо:

або

На підставі припущень теореми про допустимість рішення

(£^ц , C) – задачі x_i – ціле. Величини [x_io ], - цілі по визначенню, отже, z_i – теж ціле.

Отже, z_i певне формулою (17), ціле. Доведемо що . Доказ будемо вести від противного. Нехай .-

Це значить, що . По визначенню дробової частини . За умовою теореми x – припустиме рішення (£^ц , C) – задачі, тому . Отже,

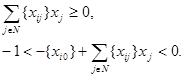
Тоді повинне виконуватися:

Отже, із припущення заперечності z_i , відразу ж одержуємо тобто z_i – неціле. Оскільки раніше було показано, що z_i , певне формулою (17), є цілим, те тим самим ми прийшли до протиріччя. Отже, припущення, що z_i < 0, невірне. Теорема доведена.

Наслідок. Будь-яке оптимальне рішення x(£, C) (£, C) – задачі, що не є припустимим рішенням (£^ц , C) – задачі, не задовольняє умові правильного відсікання (17).

Доказ. Нехай х (£, C) – оптимальне рішення (£, C) – задачі, x_i0 – дробове.

Покажемо, що х (£, C) не задовольняє умові відсікання. Оскільки план оптимальний, всі небазисні змінні x_i , для jÎN дорівнюють нулю. Тому . З огляду на це, підставимо x_io у формулу (17):

z_i (x (£, C))= – {x_i0 }+0<0 ,

що суперечить умові незаперечності z_i . Наслідок доведений.

Очевидно, що кількість додаткових обмежень буде наростати в міру рішення допоміжних (£, C) – задач, оптимальні плани яких будуть містити нецілі координати, тобто виникає проблема розмірності.

Р. Гомори запропонував прийом, що дозволяє обмежити розміри розглянутих симплексних таблиць допоміжних задач величиною (n+2) (k+1), де n – кількість змінних (£, C) – задачі, k – число небазисних змінних її. Цей прийом ґрунтується на тім, що нас цікавить додаткове обмеження лише як спосіб відсікання нецілочисленного оптимального рішення допоміжної задачі, отриманої на даному кроці, і переходу до наступної задачі.

Послідовність (£, C) – задач позначимо індексом k=0,1,…,відповідному номеру ітерації в послідовному наближенні до рішення вихідної (£^ц , C) – задачі, і позначимо (£_k , C). При цьому (£₀ , C) – задача відповідає (£, C) – задачі (задачі без вимоги цілочисленності).

Змінну z_i , що визначається додатковим лінійним обмеженням (7) і будується по деякої нецілочисленної координаті оптимального рішення (£_k , C) – задачі (k =0, 1, 2,…)позначимо x_n+k+l .

Щоб розмірність послідовності (£_k , C) – задач не зростала, викреслимо із симплекс-таблиці змінну, по якій побудоване додаткове лінійне обмеження.

Після зроблених зауважень перейдемо безпосередньо до викладу обчислювальної схеми.

1. Вирішимо (£_k , C) – задачу (спочатку k = 0) методом послідовного поліпшення плану.

Нехай у базис оптимального рішення ввійшли вектори A_s1 ,…,A_sm ... Параметри останньої симплексної таблиці позначимо через x_ij :

.

Якщо, всі базисні тридцятилітні оптимального рішення x(£_k , C) (£_k , C) – задачі цілі, то x(£_k , C) = x(£^ц , C). Якщо деяка координата x_io оптимального рішення x(£_k , C) неціла, то перейдемо до п. 2.

2. Якщо серед сукупності координат оптимального рішення x(£_k , C) є єдина неціла координата, то додаткове лінійне обмеження (17) будується по цій координаті. Якщо нецілих координат в x(£_k , C) більше однієї, то виберемо координату з найменшим номером. Нехай нею виявилася x_i0 . Складемо додаткове лінійне обмеження

(18)