Курсовая работа: Рішення задач цілочисленного програмування

де

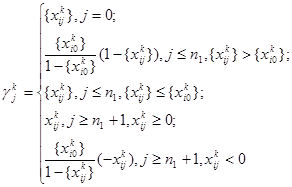(26)

визначає правильне відсікання. Блок-схема другого алгоритму Р. Гомори аналогічна блок-схемі першого алгоритму Р. Гомори й відрізняється лише правилом побудови коефіцієнтів правильного відсікання.

Правило побудови правильного відсікання

Нехай x(£_k , C) не задовольняє умові цілочисленності, – елементи симплексної таблиці, що відповідає отриманому оптимальному рішенню (£_k , C) – задачі. Виберемо i₀ =min {i | i Î (1, 2,…,n),x_i0 ^k –неціле} і будуємо правильне відсікання по формулах (24 – 26).

Умови кінцівки другого алгоритму Гомори:

1) Цільова функція F(x) задовольняє умові цілочисленності. Це враховується при виборі рядка k для побудови правильного відсікання.

2) Виконано принаймні одне із двох умов:

2') цільова функція обмежена знизу на багатогранній множині £= £₀ ;

2») задача (£₀ ^ц , C)має принаймні один план.

За допомогою другого алгоритму Гомори можна (у випадку n₁ =n) вирішувати й повністю цілочисленну задачу лінійного програмування. Однак у цьому випадку немає підстав для порівняння ефективності другого й першого алгоритмів Гомори.

5. Алгоритм Дальтона й Ллевелина

Другий алгоритм Гомори має справа із частково цілочисленними задачами лінійного програмування. Дальтон і Ллевелин розглядають широкий клас задач - частково дискретні задачі лінійного програмування й стосовно до них модифікують другий алгоритм Гомори.

Нагадаємо, що рішенням задачі дискретного програмування будемо називати вектор, координати якого належать £^ц області виду:

(27)

(28)

(29)

і максимізує значення функції

(30)

Будемо припускати, що , тобто і є наперед заданими числами.

Теорема. Нехай x(£_k , C) – оптимальне рішення задачі (27–28, 30), – елементи симплексної таблиці, що відповідає йому.

Якщо x(£_k , C) є неприпустимим рішенням задачі (27–30) і , тоді, використовуючи i-ю рядок симплексної таблиці, можна побудувати відсікання, що володіє властивістю правильності по формулах:

(31)

(32)

де

(33)

Доказ. Перевіримо спочатку умову відсікання. Нехай в оптимальному рішенні x(£_k , C) координата не задовольняє умові (29). Покажемо, що в цьому випадку вектор х(£_k , C) не задовольняє умовам (31, 32). Оскільки N_k – множина індексів небазисних змінних x_i, які в оптимальному рішенні дорівнюють нулю, то рівність (31) приймає вид і буде негативним відповідно до умови теореми. Отже, , тобто умова відсікання не виконується.

Перевіримо умову правильності. Для цього покажемо, що будь-яке припустиме рішення задачі (27-30) задовольняє умовам (31, 32).