Курсовая работа: Рішення задач цілочисленного програмування

(48)

Тому що ранг матриці дорівнює m, те

де – число елементів множини . З визначення чисел одержуємо

(49)

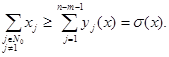(50)

З (48), (49), (50) і (46) маємо

Лема доведена при р=1 .

Тепер допустимо, що лема вірна при , і доведемо неї при :

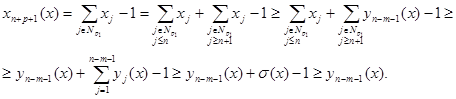
Лема доведена.

Користуючись лемою, доведемо дві теореми.

Теорема 1 . Якщо кожний оптимальний план задачі (39) – (42) містить не менш (m+2) позитивних компонентів, то алгоритм Данцига не буде кінцевим.

Доказ. Допустимо, що на s-й ітерації алгоритму Данцига вийде шуканий оптимальний план . Розглянемо числа

(51)

Всі вони цілі й серед них повинне бути (n-m ) нулів – це небазисні змінні . Крім того, за умовою серед чисел , повинне бути принаймні (m+2) позитивні числа, тобто не більше чим (n-m- 2) нулів.

По визначенню чисел звідси треба, що

а тому що повинне бути цілим, те

(52)

Але по визначенню чисел

(53)

З (52) одержуємо

(54)

і по лемі

(55)

З (52), (53) і (55) треба, що серед чисел (51) принаймні [1+(m+1)+s] = [m+2+s] позитивних, а отже, не більше чим [n+s – (m+2+s)] = (n-m-2) нулів. Але вище було відзначено, що серед чисел (51) повинне бути (n-m) нулів. Вийшло протиріччя. Теорема 1 доведена.

Наслідок (з теореми 1). Для того щоб алгоритм Данцига був кінцевим, необхідно, щоб шуканий оптимальний план лежав на ребрі багатогранної множини (40) - (41) (передбачається, що задача (39) - (41) невиродженна).