Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами

Цей вираз справедливий для довільних , і проміжків лише в тому випадку, якщо підінтегральні вирази рівні між собою. Із їх рівності випливає вираз (51).

Тепер можна вивести аналітичний вираз для ядра похибки наближення ермітовим сплайном з ланкою (1). Ядро похибки наближення многочленом степеня має вигляд . Застосувавши формулу (52), отримаємо

. (52)

Для ермітового сплайна з експоненціальною ланкою (6) ядро матиме такий вигляд:

.

А для ланки (13)

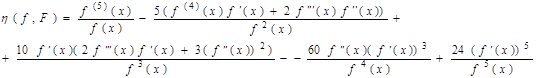
5. Рівномірне наближення ермітовими сплайнами

Наближення функції ермітовим сплайном називаємо рівномірним наближенням з заданою похибкою , якщо ,де - вага наближення,.

Алгоритм рівномірного наближення ермітовими сплайнами з заданою похибкою. Алгоритм не залежить від виду сплайна.

1. Будуємо ланку нелінійного ермітового сплайна на всьому інтервалі . Ліва границя права

2. Знаходимо похибку наближення .

3. Якщо, то наближення побудоване. Кінець.

4. Якщо , то зсуваємо праву границю інтервалу вліво, поки похибка на даному інтервалі не стане меншою від заданої похибки . Допустимо, що при -му зсуві границі вліво (т. )похибка рівна , а на попередньому кроці ( права границя ). Тоді можна знайти таку праву границю , при якій похибка буде як завгодно мало відрізнятися від заданої . Точку можна знайти одним із відомих способів, наприклад методом ділення відрізка навпіл або методом хорд.

5. Запам’ятовуємо границі ланки і параметри ермітового сплайна.

6. Лівою границею наступної ланки є права границя попередньої ланки. Правою границею можна завжди вважати т. , але можна також екстраполювати точкою де - довжина попередньої ланки.

7. Будуємо сплайн і знаходимо похибку.

8. Якщо , то переходимо до пункту 4.

9. Якщо і , то і переходимо до пункту 7. В протилежному випадку, при , запам’ятовуємо границі та параметри нелінійного ермітового сплайна. Рівномірне наближення з заданою похибкою знайдено.

Очевидно, що описаний алгоритм приводить до єдиного рішення, якщо наближувана функція і сплайн такі що функція похибки

,

є неспадною функцією від . Для цього достатньо, щоб ядро наближення при .

Із означення ермітового сплайна можна запропонувати інший алгоритм знаходження його параметрів. При (парна кількість параметрів) параметри визначаються із тих же рівнянь, що й у випадку фіксованих вузлів, до яких додаються рівняння для точки екстремумуі правої границі .

(53)

Потрібно знайти залежність від . Для деяких вузлів ланок ермітових сплайнів, а саме ланок у вигляді многочлена, відношення многочлена до лінійної функції, добутку степеневої і експоненціальної функцій, степеневого виразу від многочлена параметри сплайна знаходяться в аналітичному вигляді із перших чотирьох рівнянь системи (53).

Вони залежать від і значень функції та її похідної в цих точках. Коефіцієнти можна підставити в п’яте і шосте рівняння системи. В результаті система шести рівнянь з шістьома невідомими зводиться до системи двох рівнянь з двома невідомими :

(54)

Система (54) є системою трансцендентних рівнянь. Її можна розв’язати, використовуючи відомі наближені методи знаходження коренів трансцендентних систем.